Mathematics Questions
1. The integral ![\int \frac{1}{\sqrt[4]{(x-1)^3 (x+2)^5}} \, dx](https://s0.wp.com/latex.php?latex=%5Cint+%5Cfrac%7B1%7D%7B%5Csqrt%5B4%5D%7B%28x-1%29%5E3+%28x%2B2%29%5E5%7D%7D+%5C%2C+dx&bg=ffffff&fg=000&s=0&c=20201002) is equal to (where
is equal to (where 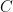 is a constant of integration):
is a constant of integration):
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
2. If ![\int_0^{100} \dfrac{\sin^2 x}{e^{\left( \frac{x}{\pi} \left[ \frac{x}{\pi} \right] \right)}} \, dx = \dfrac{\alpha \pi^3}{1 + 4\pi^2}](https://s0.wp.com/latex.php?latex=%5Cint_0%5E%7B100%7D+%5Cdfrac%7B%5Csin%5E2+x%7D%7Be%5E%7B%5Cleft%28+%5Cfrac%7Bx%7D%7B%5Cpi%7D+%5Cleft%5B+%5Cfrac%7Bx%7D%7B%5Cpi%7D+%5Cright%5D+%5Cright%29%7D%7D+%5C%2C+dx+%3D+%5Cdfrac%7B%5Calpha+%5Cpi%5E3%7D%7B1+%2B+4%5Cpi%5E2%7D&bg=ffffff&fg=000&s=0&c=20201002) ,
, 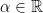 , where
, where ![[x]](https://s0.wp.com/latex.php?latex=%5Bx%5D&bg=ffffff&fg=000&s=0&c=20201002) is the greatest integer less than or equal to
is the greatest integer less than or equal to  , then the value of
, then the value of 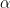 is:
is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
3. Let  be the solution of the differential equation
be the solution of the differential equation  with
with  . Then
. Then  is equal to:
is equal to:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
4. The area (in sq. units) of the region given by the set  is:
is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
5. The last common term to the sequences  (100 terms) and
(100 terms) and  (100 terms) is:
(100 terms) is:
(A) 381
(B) 521
(C) 281
(D) None
Click to View Answer
Correct Answer: [Insert Correct Option]
6. If  and
and  , where
, where 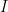 is the
is the  identity matrix, then
identity matrix, then  is equal to:
is equal to:
(A) 24
(B) 34
(C) 28
(D) 32
Click to View Answer
Correct Answer: [Insert Correct Option]
7. From a pack of 52 well-shuffled cards, cards are drawn one by one without replacement. If the  drawn card is found to be an ace, then the probability that there are no more aces left in the pack is:
drawn card is found to be an ace, then the probability that there are no more aces left in the pack is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
8. If  ,
,  ,
,  , and
, and  , then the value of
, then the value of  is equal to:
is equal to:
(A) 216
(B) 18
(C) 64
(D) None
Click to View Answer
Correct Answer: [Insert Correct Option]
9. Let 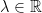 . The system of linear equations
. The system of linear equations
 is inconsistent for:
is inconsistent for:
(A) Exactly one negative value of 
(B) Exactly one positive value of 
(C) Every value of 
(D) Exactly two values of 
Click to View Answer
Correct Answer: [Insert Correct Option]
10. If the value of  is
is  , where
, where 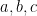 are natural numbers and
are natural numbers and  , then
, then  is equal to:
is equal to:
(A) 50
(B) 40
(C) 52
(D) 54
Click to View Answer
Correct Answer: [Insert Correct Option]
11. If the variance of the frequency distribution is 160, then the value of  is:
is:
| x | c | 2c | 3c | 4c | 5c | 6c |
| f | 2 | 1 | 1 | 1 | 1 | 1 |
(A) 5
(B) 8
(C) 7
(D) 6
Click to View Answer
Correct Answer: [Insert Correct Option]
12. Let  . Let the mean and the variance of 6 observations
. Let the mean and the variance of 6 observations  be 2 and 23, respectively. The mean deviation about the mean of these 6 observations is:
be 2 and 23, respectively. The mean deviation about the mean of these 6 observations is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
13.  . Then the range of
. Then the range of  , so that
, so that  has a maximum at
has a maximum at 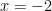 , is:
, is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
14. Let  be a function such that
be a function such that  ,
,  , and
, and  . Then which of the following is correct?
. Then which of the following is correct?
(A) 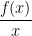 is differentiable in
is differentiable in 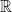
(B)  is continuous but not differentiable in
is continuous but not differentiable in 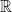
(C)  is continuous in
is continuous in 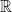
(D) None
Click to View Answer
Correct Answer: [Insert Correct Option]
15. Let  , where
, where  and
and  for all
for all  . Then the value of
. Then the value of 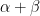 is:
is:
(A) 3
(B) 2
(C) -3
(D) 6
Click to View Answer
Correct Answer: [Insert Correct Option]
16. If ![f: [-4, 4] \to \mathbb{R}](https://s0.wp.com/latex.php?latex=f%3A+%5B-4%2C+4%5D+%5Cto+%5Cmathbb%7BR%7D&bg=ffffff&fg=000&s=0&c=20201002) , where
, where ![f(x) = \left[ \dfrac{x^4 + 1}{a} \right] \sin x + \cos x + \dfrac{e^x + e^{-x}}{2}](https://s0.wp.com/latex.php?latex=f%28x%29+%3D+%5Cleft%5B+%5Cdfrac%7Bx%5E4+%2B+1%7D%7Ba%7D+%5Cright%5D+%5Csin+x+%2B+%5Ccos+x+%2B+%5Cdfrac%7Be%5Ex+%2B+e%5E%7B-x%7D%7D%7B2%7D&bg=ffffff&fg=000&s=0&c=20201002) (where
(where ![[.]](https://s0.wp.com/latex.php?latex=%5B.%5D&bg=ffffff&fg=000&s=0&c=20201002) is the greatest integer function) is an even function, then:
is the greatest integer function) is an even function, then:
(A) ![a \in (0, 257]](https://s0.wp.com/latex.php?latex=a+%5Cin+%280%2C+257%5D&bg=ffffff&fg=000&s=0&c=20201002)
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
17. The vertices of a variable triangle are  ,
,  , and
, and  , where
, where  . The locus of its orthocenter is:
. The locus of its orthocenter is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
18. The point  is a point in the angle between the lines
is a point in the angle between the lines  and
and  containing the origin, if:
containing the origin, if:
(A)  or
or 
(B) 
(C) 
(D) None of these
Click to View Answer
Correct Answer: [Insert Correct Option]
19. In the right angle triangle as shown, an altitude is drawn from the right angle to the hypotenuse. Circles are inscribed within each of the smaller triangles. What is the distance between the centres of these circles?
(A) 5
(B) 7
(C) 8
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
20. Vector 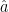 in the plane of
in the plane of  and
and  is such that it is equally inclined to
is such that it is equally inclined to  and
and  where
where  . The value of
. The value of 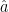 is:
is:
(A) 
(B) 
(C) 
(D) None of these
Click to View Answer
Correct Answer: [Insert Correct Option]
21. For real numbers  , and
, and 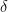 , if
, if
 where
where 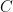 is an arbitrary constant, then the value of
is an arbitrary constant, then the value of  is equal to:
is equal to:
Click to View Answer
Correct Answer: [Insert Correct Answer]
22. The number of ways 16 identical cubes, of which 11 are blue and the rest are red, can be placed in a row so that between any two red cubes there should be at least 2 blue cubes, is:
Click to View Answer
Correct Answer: [Insert Correct Answer]
23. The number of solutions of  , where
, where 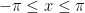 , is:
, is:
Click to View Answer
Correct Answer: [Insert Correct Answer]
24. Value of ![\lim_{x \to 0^-} \left[ \dfrac{\sin |x|}{x} \right] + \lim_{x \to 0^+} \left[ \dfrac{\sin^{-1} |x|}{|x|} \right] + \lim_{x \to 0^-} \left[ \dfrac{-2x}{\tan x} \right]](https://s0.wp.com/latex.php?latex=%5Clim_%7Bx+%5Cto+0%5E-%7D+%5Cleft%5B+%5Cdfrac%7B%5Csin+%7Cx%7C%7D%7Bx%7D+%5Cright%5D+%2B+%5Clim_%7Bx+%5Cto+0%5E%2B%7D+%5Cleft%5B+%5Cdfrac%7B%5Csin%5E%7B-1%7D+%7Cx%7C%7D%7B%7Cx%7C%7D+%5Cright%5D+%2B+%5Clim_%7Bx+%5Cto+0%5E-%7D+%5Cleft%5B+%5Cdfrac%7B-2x%7D%7B%5Ctan+x%7D+%5Cright%5D&bg=ffffff&fg=000&s=0&c=20201002) (where
(where ![[.]](https://s0.wp.com/latex.php?latex=%5B.%5D&bg=ffffff&fg=000&s=0&c=20201002) denotes the greatest integer function):
denotes the greatest integer function):
Click to View Answer
Correct Answer: [Insert Correct Answer]
25. Let a line having direction ratios  intersect the lines
intersect the lines  and
and  at the points
at the points 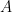 and
and 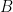 . Then
. Then  is equal to:
is equal to:
Click to View Answer
Correct Answer: [Insert Correct Answer]
