Mathematics Questions (Continued)
1. If the function  is decreasing for every
is decreasing for every ![x \in (-\infty, 0]](https://s0.wp.com/latex.php?latex=x+%5Cin+%28-%5Cinfty%2C+0%5D&bg=ffffff&fg=000&s=0&c=20201002) , then the least value of
, then the least value of  is equal to
is equal to
(A) 1
(B) 2
(C) 3
(D) 4
Click to View Answer
Correct Answer: [Insert Correct Option]
2. The  -intercept of the tangent to a curve is equal to the ordinate of the point of contact. The equation of the curve through the point
-intercept of the tangent to a curve is equal to the ordinate of the point of contact. The equation of the curve through the point 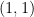 is
is
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
3. Assertion (A): If  is a relation defined on set of natural numbers
is a relation defined on set of natural numbers 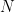 such that
such that  then
then  is an equivalence relation.
is an equivalence relation.
Reason (R): A relation is said to be an equivalence relation if it is reflexive, symmetric and transitive.
Reason (R): A relation is said to be an equivalence relation if it is reflexive, symmetric and transitive.
(A) A is True, R is True; R is a correct explanation for A.
(B) A is True, R is True; R is not a correct explanation for A.
(C) A is True, R is False
(D) A is False, R is True.
Click to View Answer
Correct Answer: [Insert Correct Option]
4. Let  be defined for
be defined for  and
and 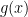 be the inverse of
be the inverse of  . If
. If  then the value of
then the value of  is
is
(A) 7
(B) 6
(C) 5
(D) 71
Click to View Answer
Correct Answer: [Insert Correct Option]
5. Let  be a non constant twice differentiable function on
be a non constant twice differentiable function on 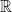 such that
such that  and
and  . Then minimum number of root(s) of equation
. Then minimum number of root(s) of equation  in
in  is/are
is/are
(A) 2
(B) 4
(C) 5
(D) 6
Click to View Answer
Correct Answer: [Insert Correct Option]
6. A circle of radius 2 units having centre in fourth quadrant passes through the vertex and focus of parabola  and touches the parabola
and touches the parabola  then the value of
then the value of  is
is
(A) 15
(B) 18
(C) 22
(D) 25
Click to View Answer
Correct Answer: [Insert Correct Option]
7. Value of  is
is
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
8. If the line  divides the area bounded by the curves
divides the area bounded by the curves  ,
,  and
and  in two regions of area
in two regions of area 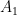 and
and  (
( ) then
) then  is equal to
is equal to
(A) 4
(B) 5
(C) 6
(D) 8
Click to View Answer
Correct Answer: [Insert Correct Option]
9. Match List-I with List-II:
| List-I | List-II |
|---|---|
| (A) Let |
(I) 16 |
| (B) |
(II) 4 |
| (C) If number of integral solution to the equation |
(III) 15 |
| (D) Let |
(IV) 14 |
(A) (A) – II, (B) – IV, (C) – IV, (D) – I
(B) (A) – I, (B) – II, (C) – I, (D) – IV
(C) (A) – II, (B) – I, (C) – IV, (D) – I
(D) (A) – IV, (B) – II, (C) – I, (D) – II
Click to View Answer
Correct Answer: [Insert Correct Option]
10. A game board is shown in the diagram below.
[Diagram: Linear Game Track with numbered squares 1-10 on top and 18-11 on bottom]
Player take turns to roll an ordinary die, then move their counter forward from ‘START’ a number of squares equal to the number rolled with the die. If a player’s counter ends its move on a cross marked square, then it is moved back to START. Let denotes the probability that player’s counter is on START after rolling the die twice and let
denotes the probability that player’s counter is on START after rolling the die twice and let 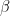 denotes the probability that after rolling the die thrice, a player’s counter is on square numbered 17, then the value of
denotes the probability that after rolling the die thrice, a player’s counter is on square numbered 17, then the value of  is
is
[Diagram: Linear Game Track with numbered squares 1-10 on top and 18-11 on bottom]
Player take turns to roll an ordinary die, then move their counter forward from ‘START’ a number of squares equal to the number rolled with the die. If a player’s counter ends its move on a cross marked square, then it is moved back to START. Let
(A) 24
(B) 21
(C) 20
(D) 18
Click to View Answer
Correct Answer: [Insert Correct Option]
11. If  then the value of
then the value of  is
is
(A) 
(B) 
(C) 0
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
12. Tangents are drawn from the point  to the hyperbola
to the hyperbola  and are inclined at angles
and are inclined at angles 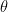 and
and 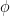 to the
to the  -axis. If
-axis. If  then value of
then value of  is
is
(A) 7
(B) -7
(C) 1
(D) -1
Click to View Answer
Correct Answer: [Insert Correct Option]
13. Let  . Then value of
. Then value of  is
is
(A) 40
(B) 42
(C) 38
(D) 84
Click to View Answer
Correct Answer: [Insert Correct Option]
14. Let  be polynomial
be polynomial  where
where  . If
. If  and
and  . Which of the following is a possible value of
. Which of the following is a possible value of  .
.
(A) -27
(B) -18
(C) -6
(D) -3
Click to View Answer
Correct Answer: [Insert Correct Option]
15. Statement-I: Let  be matrix of order
be matrix of order  and
and  . If
. If  and
and 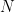 are matrices of order
are matrices of order  such that
such that  then
then  . (where
. (where  denotes determinant of matrix
denotes determinant of matrix 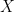 ;
;  denotes adjoint of matrix
denotes adjoint of matrix 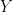 )
)
Statement-II: If is non-singular square matrix of order
is non-singular square matrix of order  then
then 
Statement-II: If
(A) Statement-I is true, Statement-II is false.
(B) Statement-I is false, Statement-II is true.
(C) Statement-I is true, Statement-II is true.
(D) Statement-I is false, Statement-II is false.
Click to View Answer
Correct Answer: [Insert Correct Option]
16. Let  and
and ![g: (-2, 2) \to \mathbb{R}, g(x) = [x] |x^2 - 1| + \sin \left( \frac{\pi}{[x] + 3} \right) - [x + 1]](https://s0.wp.com/latex.php?latex=g%3A+%28-2%2C+2%29+%5Cto+%5Cmathbb%7BR%7D%2C+g%28x%29+%3D+%5Bx%5D+%7Cx%5E2+-+1%7C+%2B+%5Csin+%5Cleft%28+%5Cfrac%7B%5Cpi%7D%7B%5Bx%5D+%2B+3%7D+%5Cright%29+-+%5Bx+%2B+1%5D&bg=ffffff&fg=000&s=0&c=20201002) . If ‘
. If ‘ ‘ denotes number of points where
‘ denotes number of points where  is not differentiable and ‘
is not differentiable and ‘ ‘ denotes the number of points where
‘ denotes the number of points where 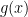 is discontinuous then
is discontinuous then  is (where
is (where ![[.]](https://s0.wp.com/latex.php?latex=%5B.%5D&bg=ffffff&fg=000&s=0&c=20201002) denotes the Greatest Integer Function)
denotes the Greatest Integer Function)
(A) 3
(B) 2
(C) 4
(D) 6
Click to View Answer
Correct Answer: [Insert Correct Option]
17. Equation of plane which passes through the point of intersection of the lines  and
and  and has the largest distance from the origin is
and has the largest distance from the origin is  then
then  is
is
(A) 12
(B) 7
(C) 15
(D) 5
Click to View Answer
Correct Answer: [Insert Correct Option]
18. Let  be a real valued function such that
be a real valued function such that  . If
. If  and
and  are the maximum and minimum values of the function
are the maximum and minimum values of the function  respectively then
respectively then  is
is
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
19. An online exam is attempted by 50 candidates out of which 20 are boys. The average marks obtained by boys is 12 with a variance 2. The variance of marks obtained by 30 girls is also 2. The average marks of all 50 candidates is 15. If 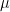 is the average marks of girls and
is the average marks of girls and 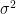 is the variance of marks of all 50 candidates, then
is the variance of marks of all 50 candidates, then  is equal to
is equal to
(A) 25
(B) 20
(C) 15
(D) 30
Click to View Answer
Correct Answer: [Insert Correct Option]
20. Let  be the root of
be the root of  . For some values of ‘
. For some values of ‘ ‘, if
‘, if  where
where  is orthocentre of triangle with
is orthocentre of triangle with  and
and  as co-ordinates of its vertices. Then sum of possible values of
as co-ordinates of its vertices. Then sum of possible values of  is
is
(A) 33
(B) 15
(C) 35
(D) 23
Click to View Answer
Correct Answer: [Insert Correct Option]
21. Let  and
and  be the set of words which can be formed using all the letters of the words SHREYANSH and SANIDHYA respectively. A set is randomly chosen and a word is selected at random from it. If the probability that it contains at least one pair of alike letters together is
be the set of words which can be formed using all the letters of the words SHREYANSH and SANIDHYA respectively. A set is randomly chosen and a word is selected at random from it. If the probability that it contains at least one pair of alike letters together is  (where
(where  and
and  are coprime) then the value of
are coprime) then the value of  is
is
Click to View Answer
Correct Answer: [Insert Correct Answer]
22. Let  be the vectors representing three coterminous edges of tetrahedron such that
be the vectors representing three coterminous edges of tetrahedron such that  and
and  . If
. If 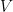 is volume of the tetrahedron, then the maximum value of
is volume of the tetrahedron, then the maximum value of 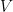 is (where
is (where  represent angle between
represent angle between 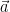 and
and  )
)
Click to View Answer
Correct Answer: [Insert Correct Answer]
23. If the complete set of values of ‘ ‘ for which the function
‘ for which the function  defined by
defined by  is strictly increasing is
is strictly increasing is ![[p, q]](https://s0.wp.com/latex.php?latex=%5Bp%2C+q%5D&bg=ffffff&fg=000&s=0&c=20201002) (where
(where 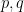 are integers) then
are integers) then  is
is
Click to View Answer
Correct Answer: [Insert Correct Answer]
24. Let  denotes
denotes  digit number where the first and last digit are 7 and the remaining
digit number where the first and last digit are 7 and the remaining  digits are 5. Consider the sum
digits are 5. Consider the sum  . If
. If  , then
, then 
Click to View Answer
Correct Answer: [Insert Correct Answer]
25. A point  moves in xy plane in such a way that
moves in xy plane in such a way that  . Area of region representing all possible of point
. Area of region representing all possible of point  is equal to
is equal to
Click to View Answer
Correct Answer: [Insert Correct Answer]
