Mathematics Questions
1. If all interior angle of quadrilateral are in A.P. If common difference is  , then find smallest angle?
, then find smallest angle?
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
2. If 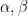 are the roots of
are the roots of  , then the roots of equation
, then the roots of equation  are :-
are :-
(A) 
(B) 
(C) 
(D) 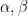
Click to View Answer
Correct Answer: [Insert Correct Option]
3. Let  such that
such that  , if system of equations
, if system of equations
 has a non-trivial solutions then –
has a non-trivial solutions then –
(A) 
(B) 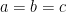
(C) 
(D) None of these
Click to View Answer
Correct Answer: [Insert Correct Option]
4. If  is divided by 11, then the remainder is
is divided by 11, then the remainder is
(A) 1
(B) 3
(C) 5
(D) 8
Click to View Answer
Correct Answer: [Insert Correct Option]
5. There are two bags, one of which contain 3 black and 4 white balls while the second contains 4 black and 3 white balls. A dice is cast, if the face 1 or 3 turns up, a ball is taken from the first bag, and if any other face turn up, a ball is taken from second bag, then find the probability of choosing a black ball :-
(A) 
(B) 
(C) 
(D) None of these
Click to View Answer
Correct Answer: [Insert Correct Option]
6. If  \& if
\& if  , then the value of
, then the value of  must be
must be
(A) 35
(B) 1225
(C) 225
(D) 2
Click to View Answer
Correct Answer: [Insert Correct Option]
7. If  and
and  , then standard deviation of observations
, then standard deviation of observations  and
and  is equal to-
is equal to-
(A) 8
(B) 16
(C) 4
(D) 2
Click to View Answer
Correct Answer: [Insert Correct Option]
8. The mean and the standard deviation (s.d.) of 10 observations are 20 and 2 respectively. Each of these 10 observations is multiplied by  and then reduced by
and then reduced by  , where
, where  and
and  . If the new mean and new s.d. become half of their original values, then
. If the new mean and new s.d. become half of their original values, then  is equal to
is equal to
(A) 
(B) 10
(C) 
(D) 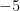
Click to View Answer
Correct Answer: [Insert Correct Option]
9. Let  , where
, where  is an even number, then for
is an even number, then for ![x \in [0, 2\pi]](https://s0.wp.com/latex.php?latex=x+%5Cin+%5B0%2C+2%5Cpi%5D&bg=ffffff&fg=000&s=0&c=20201002) , number of maxima and minima are
, number of maxima and minima are  and
and  respectively, then-
respectively, then-
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
10. Given  (where
(where ![[.], \{.\}](https://s0.wp.com/latex.php?latex=%5B.%5D%2C+%5C%7B.%5C%7D&bg=ffffff&fg=000&s=0&c=20201002) and
and  denotes greatest integer function, fractional part function and signum function respectively)
denotes greatest integer function, fractional part function and signum function respectively)
(A)  is continuous at
is continuous at 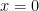 if
if 
(B) for  ,
,  has removable discontinuity at
has removable discontinuity at 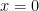
(C) for  ,
,  has non-removable discontinuity at
has non-removable discontinuity at 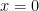
(D)  exists
exists
Click to View Answer
Correct Answer: [Insert Correct Option]
11. If  and
and 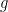 is the inverse function of
is the inverse function of  , then the value of
, then the value of  at
at 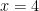 equals :
equals :
(A) 
(B) 
(C) 3
(D) 6
Click to View Answer
Correct Answer: [Insert Correct Option]
12. If  is a polynomial such that :-
is a polynomial such that :-  and
and  then value of
then value of ![f\left(\sqrt[3]{\frac{1}{5^{\log 7}} + \frac{1}{\sqrt{-\log_{10}(0.1)}}}\right)](https://s0.wp.com/latex.php?latex=f%5Cleft%28%5Csqrt%5B3%5D%7B%5Cfrac%7B1%7D%7B5%5E%7B%5Clog+7%7D%7D+%2B+%5Cfrac%7B1%7D%7B%5Csqrt%7B-%5Clog_%7B10%7D%280.1%29%7D%7D%7D%5Cright%29&bg=ffffff&fg=000&s=0&c=20201002) :-
:-
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
13. 
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
14.  is equal to :-
is equal to :-
(A) 
(B) 
(C) 
(D) None of these
Click to View Answer
Correct Answer: [Insert Correct Option]
15. The area (in sq. units) of the region  is :-
is :-
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
16. The solution of the differential equation  is :
is :
(A) 
(B) 
(C) 
(D) None of these
Click to View Answer
Correct Answer: [Insert Correct Option]
17. A ray of light coming from the point  gets reflected from the point
gets reflected from the point 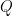 on the
on the  -axis and then passes through the point
-axis and then passes through the point  . If the point
. If the point  is such that
is such that 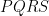 is a parallelogram, then
is a parallelogram, then  is equal to :
is equal to :
(A) 80
(B) 90
(C) 60
(D) 70
Click to View Answer
Correct Answer: [Insert Correct Option]
18. Let  ,
,  and
and  , where
, where 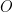 is the origin. If the area of the parallelogram with adjacent sides
is the origin. If the area of the parallelogram with adjacent sides  and
and  is 15 sq. units, then the area (in sq. units) of the quadrilateral
is 15 sq. units, then the area (in sq. units) of the quadrilateral  is equal to :
is equal to :
(A) 38
(B) 40
(C) 32
(D) 35
Click to View Answer
Correct Answer: [Insert Correct Option]
19. The shortest distance between the line
 is :
is :
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
20. Let the circles  and
and  touch each other externally at the point
touch each other externally at the point  . If the point
. If the point  divides the line segment joining the centres of the circles
divides the line segment joining the centres of the circles 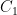 and
and  internally in the ratio
internally in the ratio  , then
, then  equals
equals
(A) 110
(B) 130
(C) 125
(D) 145
Click to View Answer
Correct Answer: [Insert Correct Option]
21. The number of 5-digit numbers of the form  in which
in which  is :-
is :-
Click to View Answer
Correct Answer: [Insert Correct Answer]
22. If  and
and
 and
and  and
and 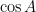 are roots of equation
are roots of equation  . Then value of
. Then value of  is :-
is :-
Click to View Answer
Correct Answer: [Insert Correct Answer]
23. If  exists and is equal to
exists and is equal to 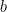 , then the value of
, then the value of  is
is
Click to View Answer
Correct Answer: [Insert Correct Answer]
24. If  ; then value of
; then value of 
Click to View Answer
Correct Answer: [Insert Correct Answer]
25. Let the foci of a hyperbola  coincide with the foci of the ellipse
coincide with the foci of the ellipse  and the eccentricity of the hyperbola
and the eccentricity of the hyperbola  be the reciprocal of the eccentricity of the ellipse
be the reciprocal of the eccentricity of the ellipse 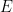 . If the length of the transverse axis of
. If the length of the transverse axis of  is
is  and the length of its conjugate axis is
and the length of its conjugate axis is 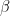 , then
, then  is equal to :
is equal to :
Click to View Answer
Correct Answer: [Insert Correct Answer]
