SECTION A: Multiple Choice Questions
1. Number of rational terms in the expansion of  is:
is:
(A) 7
(B) 8
(C) 9
(D) 10
Click to View Answer
Correct Answer: [Insert Correct Option]
2. The least value of  occurs when
occurs when  (Where
(Where 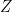 is complex no.)
is complex no.)
(A) 
(B) 
(C) 
(D) None of these
Click to View Answer
Correct Answer: [Insert Correct Option]
3. Let 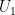 and
and 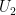 be two bags such that
be two bags such that 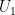 contains 3 white and 2 red balls and
contains 3 white and 2 red balls and 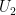 contains only 1 white ball. A fair coin is tossed if head appears, then 1 ball is drawn at random from
contains only 1 white ball. A fair coin is tossed if head appears, then 1 ball is drawn at random from 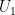 and put into
and put into 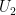 . However if tail appears, then 2 balls are drawn at random from
. However if tail appears, then 2 balls are drawn at random from 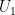 and put into
and put into 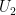 . Now, 1 ball is drawn at random from
. Now, 1 ball is drawn at random from 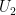 then. The probability of the drawn ball from
then. The probability of the drawn ball from 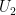 being white is :-
being white is :-
(A) 
(B) 
(C) 
(D) 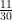
Click to View Answer
Correct Answer: [Insert Correct Option]
4. For  , let
, let  satisfies
satisfies  . Also the
. Also the  has only one real solution then
has only one real solution then  is equal to :-
is equal to :-
(A) 4
(B) 5
(C) 6
(D) 7
Click to View Answer
Correct Answer: [Insert Correct Option]
5. If  is a square matrix of order 4 and
is a square matrix of order 4 and  , where
, where  , then value of
, then value of  is :
is :
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
6. The function  attains its maximum at
attains its maximum at  is equal to :-
is equal to :-
(A) 1
(B) 2
(C) 3
(D) 4
Click to View Answer
Correct Answer: [Insert Correct Option]
7. A spherical balloon is expanding. If at any instant rate of increase of its volume is 16 times of rate of increase of its radius, then its radius at that instant, is :
(A) 
(B) 
(C) 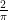
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
8. If  is a polynomial in a real variable
is a polynomial in a real variable  , then
, then  has
has
(A) neither a maximum nor a minimum
(B) only one maximum
(C) only one minimum
(D) None of these
Click to View Answer
Correct Answer: [Insert Correct Option]
9. If  is continuous in the interval
is continuous in the interval ![[-1, 1]](https://s0.wp.com/latex.php?latex=%5B-1%2C+1%5D&bg=ffffff&fg=000&s=0&c=20201002) then
then  equals
equals
(A) 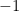
(B) 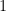
(C) 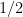
(D) 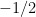
Click to View Answer
Correct Answer: [Insert Correct Option]
10. The area of the bounded region enclosed by the curve  and the
and the  -axis is :
-axis is :
(A) 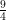
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
11.  Where
Where  denotes greatest integer less than or equal to
denotes greatest integer less than or equal to 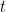 , is equal to :
, is equal to :
(A) 
(B) 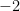
(C) 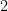
(D) 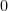
Click to View Answer
Correct Answer: [Insert Correct Option]
12. Let the solution curve  of the differential equation,
of the differential equation, ![\left[ \frac{x}{\sqrt{x^2 - y^2}} + e^{\frac{y}{x}} \right] \frac{dy}{dx} = x + \left[ \frac{x}{\sqrt{x^2 - y^2}} + e^{\frac{y}{x}} \right] y](https://s0.wp.com/latex.php?latex=%5Cleft%5B+%5Cfrac%7Bx%7D%7B%5Csqrt%7Bx%5E2+-+y%5E2%7D%7D+%2B+e%5E%7B%5Cfrac%7By%7D%7Bx%7D%7D+%5Cright%5D+%5Cfrac%7Bdy%7D%7Bdx%7D+%3D+x+%2B+%5Cleft%5B+%5Cfrac%7Bx%7D%7B%5Csqrt%7Bx%5E2+-+y%5E2%7D%7D+%2B+e%5E%7B%5Cfrac%7By%7D%7Bx%7D%7D+%5Cright%5D+y&bg=ffffff&fg=000&s=0&c=20201002) pass through the points
pass through the points 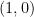 and
and  . Then
. Then  is
is  equal to
equal to
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
13.  , Where
, Where 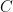 is a constant, then
is a constant, then  at
at  is equal to :
is equal to :
(A) 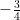
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
14. If  and
and  , where
, where  and
and  , then the value of
, then the value of  and the quadrant in which
and the quadrant in which 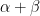 lies, respectively are :
lies, respectively are :
(A)  and IV
and IV quadrant
quadrant
(B) 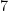 and I
and I quadrant
quadrant
(C)  and IV
and IV quadrant
quadrant
(D) 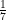 and I
and I quadrant
quadrant
Click to View Answer
Correct Answer: [Insert Correct Option]
15. The value of  is equal to :
is equal to :
(A) 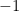
(B) 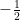
(C) 
(D) 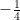
Click to View Answer
Correct Answer: [Insert Correct Option]
16. If the mean deviation about median for the number 3, 5, 7, 2k, 12, 16, 21, 24 arranged in the ascending order, is 6 then the median is
(A) 11.5
(B) 10.5
(C) 12
(D) 11
Click to View Answer
Correct Answer: [Insert Correct Option]
17. Maximum distance of any point on the curve  from the origin is :-
from the origin is :-
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
18. In the right angle triangle as shown, an altitude is drawn from the right to the hypotenuse. Circles are inscribed within each of the smaller triangles. What is the distance between the centres of these circles ?
[Diagram: Right-angled triangle with sides 15, 20 and inscribed circles in sub-triangles]
[Diagram: Right-angled triangle with sides 15, 20 and inscribed circles in sub-triangles]
(A) 5
(B) 7
(C) 8
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
19. The foci of the ellipse  and those of hyperbola
and those of hyperbola  coincide then
coincide then 
(A) 3
(B) 7
(C) 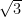
(D) 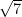
Click to View Answer
Correct Answer: [Insert Correct Option]
20. The distance of the point having position vector  from the straight line passing through the point
from the straight line passing through the point  and parallel to the vector,
and parallel to the vector,  is :
is :
(A) 7
(B) 
(C) 
(D) 6
Click to View Answer
Correct Answer: [Insert Correct Option]
21. If  and
and  , then the minimum value of
, then the minimum value of  is equal to :
is equal to :
Click to View Answer
Correct Answer: [Insert Correct Answer]
22. Let  be a twice-differentiable function and
be a twice-differentiable function and  . Then evaluate.
. Then evaluate.

Click to View Answer
Correct Answer: [Insert Correct Answer]
23. For real numbers  , let
, let
 and
and
 .
Then the value of
.
Then the value of  is equal to.
is equal to.
Click to View Answer
Correct Answer: [Insert Correct Answer]
24. Suppose a class has 7 students. The average marks of these students in the mathematics examination is 62, and their variance is 20. A student fails in the examination if he/she gets less than 50 marks, then in the worst case, the number of students can fail is :
Click to View Answer
Correct Answer: [Insert Correct Answer]
25. Consider the set of eight vectors
 .
Three non-coplanar vectors can be chosen from
.
Three non-coplanar vectors can be chosen from 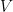 in
in  ways. Then
ways. Then  is .
is .
Click to View Answer
Correct Answer: [Insert Correct Answer]
