SECTION A: Multiple Choice Questions
1. If  , then minimum value of the expression
, then minimum value of the expression  is:
is:
(A) 4
(B) 3
(C) 5
(D) 6
Click to View Answer
Correct Answer: [Insert Correct Answer]
2. The value of  is equal to:
is equal to:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Answer]
3. If  and
and  , then standard deviation of observations
, then standard deviation of observations  and
and  is equal to:
is equal to:
(A) 8
(B) 16
(C) 4
(D) 2
Click to View Answer
Correct Answer: [Insert Correct Answer]
4. If  is a complex number satisfying
is a complex number satisfying  , then range of
, then range of  is (where
is (where  ):
):
(A) ![[5 - 3\sqrt{2}, 5 + 3\sqrt{2}]](https://s0.wp.com/latex.php?latex=%5B5+-+3%5Csqrt%7B2%7D%2C+5+%2B+3%5Csqrt%7B2%7D%5D&bg=ffffff&fg=000&s=0&c=20201002)
(B) ![[3\sqrt{2} - 5, 3\sqrt{2} + 5]](https://s0.wp.com/latex.php?latex=%5B3%5Csqrt%7B2%7D+-+5%2C+3%5Csqrt%7B2%7D+%2B+5%5D&bg=ffffff&fg=000&s=0&c=20201002)
(C) ![[0, 5 + 3\sqrt{2}]](https://s0.wp.com/latex.php?latex=%5B0%2C+5+%2B+3%5Csqrt%7B2%7D%5D&bg=ffffff&fg=000&s=0&c=20201002)
(D) ![[0, 5 - 3\sqrt{2}]](https://s0.wp.com/latex.php?latex=%5B0%2C+5+-+3%5Csqrt%7B2%7D%5D&bg=ffffff&fg=000&s=0&c=20201002)
Click to View Answer
Correct Answer: [Insert Correct Answer]
5. If matrix ![A = [a_{ij}]_{3 \times 3}](https://s0.wp.com/latex.php?latex=A+%3D+%5Ba_%7Bij%7D%5D_%7B3+%5Ctimes+3%7D&bg=ffffff&fg=000&s=0&c=20201002) and
and  and element
and element  , then number of matrix
, then number of matrix  is equal to:
is equal to:
(A) 3370
(B) 3300
(C) 3375
(D) None of these
Click to View Answer
Correct Answer: [Insert Correct Answer]
6. A box contains 10 tickets numbered from 1 to 10. Two tickets are drawn one by one with replacement. The probability that the “difference between the first drawn ticket number and second is not less than 4” is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Answer]
7.  &
&  when divided by 4 leaves a remainder of 0, 1 & 2 respectively. Find number of non-negative integral solution of the equation
when divided by 4 leaves a remainder of 0, 1 & 2 respectively. Find number of non-negative integral solution of the equation  :
:
(A) 45
(B) 55
(C) 105
(D) 190
Click to View Answer
Correct Answer: [Insert Correct Answer]
8. Two data sets each of size 10 has the variance as 4 and 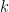 and the corresponding means as 2 and 4 respectively. If the variance of the combined data set is 5.5, then the value of
and the corresponding means as 2 and 4 respectively. If the variance of the combined data set is 5.5, then the value of 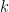 is equal to:
is equal to:
(A) 5
(B) 6
(C) 4
(D) 3
Click to View Answer
Correct Answer: [Insert Correct Answer]
9. If  and
and 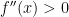 ,
, 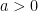 ,
,  , then:
, then:
(A) 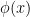 increases in
increases in 
(B) 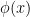 increases in
increases in 
(C) 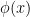 decreases in
decreases in 
(D) None
Click to View Answer
Correct Answer: [Insert Correct Answer]
10. The global maximum value of  ,
, ![x \in [2, 3]](https://s0.wp.com/latex.php?latex=x+%5Cin+%5B2%2C+3%5D&bg=ffffff&fg=000&s=0&c=20201002) , is:
, is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Answer]
11. Let  be a function such that
be a function such that  ,
,  and
and  , then which of the following is correct?
, then which of the following is correct?
(A) 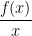 is differentiable in
is differentiable in 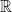
(B)  is continuous but not differentiable in
is continuous but not differentiable in 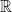
(C)  is continuous in
is continuous in 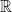
(D) None
Click to View Answer
Correct Answer: [Insert Correct Answer]
12. If  , then at
, then at 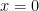 :
:
(A)  is continuous, when
is continuous, when 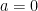
(B)  is continuous, when
is continuous, when 
(C)  is discontinuous for every value of
is discontinuous for every value of 
(D) None of these
Click to View Answer
Correct Answer: [Insert Correct Answer]
13. Area bounded by  and
and  , is:
, is:
(A) 32
(B) 16
(C) 64
(D) 8
Click to View Answer
Correct Answer: [Insert Correct Answer]
14. A curve passes through the point  . Let the slope of the curve at each point
. Let the slope of the curve at each point 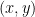 be
be  ,
,  . Then the equation of the curve is:
. Then the equation of the curve is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Answer]
15. If  , then the value of
, then the value of  is:
is:
(A) -1
(B) 1
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Answer]
16.  where
where 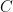 is constant of integration and
is constant of integration and  ,
,  , then:
, then:
(A) 
(B)  (in order) are in arithmetic progression
(in order) are in arithmetic progression
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Answer]
17. Area of the triangle 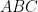 where
where  ,
,  and
and 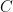 lies on
lies on  is equal to:
is equal to:
(A) 
(B) 26
(C) 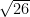
(D) 
Click to View Answer
Correct Answer: [Insert Correct Answer]
18. If a circle of radius  passes through the origin
passes through the origin 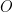 and intersects the coordinate axes at
and intersects the coordinate axes at  and
and  , then the locus of the foot of perpendicular from
, then the locus of the foot of perpendicular from 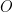 on
on  is:
is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Answer]
19. The slope of the line which belongs to family of lines  and makes shortest intercept on
and makes shortest intercept on  is:
is:
(A) 
(B) 0
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Answer]
20. The equation of the line of shortest distance of the lines  and
and 
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Answer]
SECTION B: Numerical Value Type Questions
21. Mean and median of four numbers 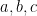 and
and  (
( ) is 35 and 25 respectively then the value of
) is 35 and 25 respectively then the value of  will be:
will be:
Click to View Answer
Correct Answer: [Insert Integer Value]
22. The  term in the expansion of
term in the expansion of  is independent of
is independent of  then the sum of the divisors of
then the sum of the divisors of  is:
is:
Click to View Answer
Correct Answer: [Insert Integer Value]
23. Let  be twice differentiable function and
be twice differentiable function and  , then
, then  is equal to:
is equal to:
Click to View Answer
Correct Answer: [Insert Integer Value]
24. Let  be defined as
be defined as ![f(x) = \begin{cases} x - [x], & \text{if } [x] \text{ is odd} \\ x - [x + 2], & \text{if } [x] \text{ is even} \end{cases}](https://s0.wp.com/latex.php?latex=f%28x%29+%3D+%5Cbegin%7Bcases%7D+x+-+%5Bx%5D%2C+%26+%5Ctext%7Bif+%7D+%5Bx%5D+%5Ctext%7B+is+odd%7D+%5C%5C+x+-+%5Bx+%2B+2%5D%2C+%26+%5Ctext%7Bif+%7D+%5Bx%5D+%5Ctext%7B+is+even%7D+%5Cend%7Bcases%7D&bg=ffffff&fg=000&s=0&c=20201002) , if
, if  is
is 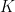 then find the value
then find the value ![[K]](https://s0.wp.com/latex.php?latex=%5BK%5D&bg=ffffff&fg=000&s=0&c=20201002) ?
?
[Note:![[K]](https://s0.wp.com/latex.php?latex=%5BK%5D&bg=ffffff&fg=000&s=0&c=20201002) denotes greatest integer less than or equal to
denotes greatest integer less than or equal to 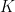 ]
]
[Note:
Click to View Answer
Correct Answer: [Insert Integer Value]
25. If  , then the value of
, then the value of  equals (where
equals (where 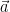 ,
,  and
and  are unit vectors):
are unit vectors):
Click to View Answer
Correct Answer: [Insert Integer Value]
