SECTION A: Multiple Choice Questions
1. If all interior angles of a quadrilateral are in A.P. with a common difference of  , then find the smallest angle.
, then find the smallest angle.
(A) 
(B) 
(C) 
(D) 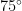
Click to View Answer
Correct Answer: [Insert Correct Answer]
2. If 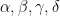 are the roots of
are the roots of  then
then  is equal to:
is equal to:
(A) 
(B) 
(C) 4
(D) 
Click to View Answer
Correct Answer: [Insert Correct Answer]
3. If  are the angles of triangle and the system of equations has non-trivial solutions:
are the angles of triangle and the system of equations has non-trivial solutions:



then the triangle is necessarily:
then the triangle is necessarily:
(A) Equilateral 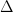
(B) Acute angled 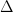
(C) Isosceles 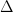
(D) Right angled 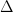
Click to View Answer
Correct Answer: [Insert Correct Answer]
4. The probability that in a family of 5 members, exactly two members have birthday on Sunday is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Answer]
5. If  , then locus of
, then locus of  is:
is:
(A) a straight line
(B) a circle having centre on  -axis
-axis
(C) a circle having centre on 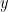 -axis
-axis
(D) a parabola
Click to View Answer
Correct Answer: [Insert Correct Answer]
6.  is equal to:
is equal to:
(A) 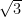
(B) 
(C) 3
(D) 
Click to View Answer
Correct Answer: [Insert Correct Answer]
7. Let the mean and the variance of 5 observations  be
be  and
and  respectively. If the mean and variance of the first 4 observations are
respectively. If the mean and variance of the first 4 observations are  and
and  respectively, then
respectively, then  is equal to:
is equal to:
(A) 13
(B) 15
(C) 17
(D) 18
Click to View Answer
Correct Answer: [Insert Correct Answer]
8. The mean and variance of the data 4, 5, 6, 6, 7, 8,  where
where  are 6, and
are 6, and  respectively. Then
respectively. Then  is equal to:
is equal to:
(A) 162
(B) 320
(C) 674
(D) 420
Click to View Answer
Correct Answer: [Insert Correct Answer]
9. If 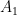 and
and  are areas bounded by:
are areas bounded by:
 and
and 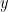 -axis in
-axis in  quadrant.
quadrant.
 and
and  -axis and
-axis and  , then:
, then:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Answer]
10. Value of  is equal to:
is equal to:
(A) 7
(B) -7
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Answer]
11. Solution of differential equation  is:
is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Answer]
12. If  , then:
, then:
(A) 
(B) 
(C) 
(D) None of these
Click to View Answer
Correct Answer: [Insert Correct Answer]
13. Range of  (where
(where  denotes greatest integer less than or equal to
denotes greatest integer less than or equal to  ).
).
(A) ![[0, \pi]](https://s0.wp.com/latex.php?latex=%5B0%2C+%5Cpi%5D&bg=ffffff&fg=000&s=0&c=20201002)
(B) ![[-1, 1]](https://s0.wp.com/latex.php?latex=%5B-1%2C+1%5D&bg=ffffff&fg=000&s=0&c=20201002)
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Answer]
14. If  is continuous at
is continuous at 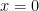 then find
then find 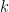 :
:
(A) 2
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Answer]
15. Let  be a differentiable function having
be a differentiable function having  . Then
. Then  equals:
equals:
(A) 24
(B) 18
(C) 12
(D) None of these
Click to View Answer
Correct Answer: [Insert Correct Answer]
16. If  and
and  , then:
, then:
(A) 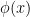 increases in
increases in 
(B) 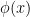 increases in
increases in 
(C) 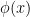 decreases in
decreases in 
(D) None
Click to View Answer
Correct Answer: [Insert Correct Answer]
17. The straight line  meets the coordinate axes at
meets the coordinate axes at  and
and  . A circle is drawn through
. A circle is drawn through  ,
,  and the origin. Then the sum of perpendicular distances from
and the origin. Then the sum of perpendicular distances from  and
and  on the tangent to the circle at the origin is:
on the tangent to the circle at the origin is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Answer]
18. From the point  tangents are drawn to parabola
tangents are drawn to parabola  , then the area of the triangle formed by the chord of contact and the tangent is:
, then the area of the triangle formed by the chord of contact and the tangent is:
(A) 
(B) 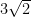
(C) 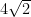
(D) 
Click to View Answer
Correct Answer: [Insert Correct Answer]
19. The eccentricity of the ellipse with centre at the origin which meets the straight line  on the axis of
on the axis of  and the straight line
and the straight line  on the axis of
on the axis of 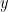 and whose axes lie along the axes of coordinates is:
and whose axes lie along the axes of coordinates is:
(A) 
(B) 
(C) 
(D) None of these
Click to View Answer
Correct Answer: [Insert Correct Answer]
20. Vector  is perpendicular to
is perpendicular to  and
and  is perpendicular to
is perpendicular to  . The angle between non zero vectors
. The angle between non zero vectors 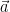 &
&  is:
is:
(A) 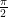
(B) 
(C) 
(D) data Insufficient
Click to View Answer
Correct Answer: [Insert Correct Answer]
SECTION B: Numerical Value Type Questions
21. Number of ways in which AAABBB can be placed in the squares of figure as shown so that no row remains empty is ?
[Insert Your Image Here]
Click to View Answer
Correct Answer: [Insert Correct Answer]
22. If  , then
, then  is equal to…
is equal to…
Click to View Answer
Correct Answer: [Insert Correct Answer]
23.  where
where  , then
, then  is equal to…
is equal to…
(where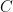 is constant of integration)
is constant of integration)
(where
Click to View Answer
Correct Answer: [Insert Correct Answer]
24. The integer  for which
for which  is a finite non-zero number, is…
is a finite non-zero number, is…
Click to View Answer
Correct Answer: [Insert Correct Answer]
25. The projection of the line segment joining the points  and
and  on the line joining the points
on the line joining the points  and
and  is…
is…
Click to View Answer
Correct Answer: [Insert Correct Answer]
