SECTION A: Multiple Choice Questions
1. If ![x \sin \left( \dfrac{y}{x} \right) dy = \left[ y \sin \left( \dfrac{y}{x} \right) - x \right] dx](https://s0.wp.com/latex.php?latex=x+%5Csin+%5Cleft%28+%5Cdfrac%7By%7D%7Bx%7D+%5Cright%29+dy+%3D+%5Cleft%5B+y+%5Csin+%5Cleft%28+%5Cdfrac%7By%7D%7Bx%7D+%5Cright%29+-+x+%5Cright%5D+dx&bg=ffffff&fg=000&s=0&c=20201002) and
and  , then
, then  is equal to:
is equal to:
(A) 
(B) 
(C) 
(D) 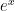
Click to View Answer
Correct Answer: [Insert Correct Option]
2. If the integral ![\int_{0}^{10} \dfrac{[\sin 2\pi x]}{e^{x - [x]}} \, dx = \alpha e^{-1} + \beta e^{\dfrac{1}{2}} + \gamma](https://s0.wp.com/latex.php?latex=%5Cint_%7B0%7D%5E%7B10%7D+%5Cdfrac%7B%5B%5Csin+2%5Cpi+x%5D%7D%7Be%5E%7Bx+-+%5Bx%5D%7D%7D+%5C%2C+dx+%3D+%5Calpha+e%5E%7B-1%7D+%2B+%5Cbeta+e%5E%7B%5Cdfrac%7B1%7D%7B2%7D%7D+%2B+%5Cgamma&bg=ffffff&fg=000&s=0&c=20201002) , where
, where  are integers and
are integers and ![[x]](https://s0.wp.com/latex.php?latex=%5Bx%5D&bg=ffffff&fg=000&s=0&c=20201002) denotes the greatest integer less than or equal to
denotes the greatest integer less than or equal to  , then the value of
, then the value of  is equal to:
is equal to:
(A) 0
(B) 20
(C) 25
(D) 10
Click to View Answer
Correct Answer: [Insert Correct Option]
3. ![\int \dfrac{dx}{\sqrt[4]{(x-1)^3 (x+2)^5}}](https://s0.wp.com/latex.php?latex=%5Cint+%5Cdfrac%7Bdx%7D%7B%5Csqrt%5B4%5D%7B%28x-1%29%5E3+%28x%2B2%29%5E5%7D%7D&bg=ffffff&fg=000&s=0&c=20201002) is equal to:
is equal to:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
4. The area of the shorter region bounded by  and
and  is given by
is given by  sq-unit where
sq-unit where 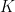 is equal to:
is equal to:
(A) 1
(B) 2
(C) 3
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
5. Let  and
and  . Then find the interval in which
. Then find the interval in which 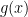 increases:
increases:
(A) 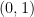
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
6. If  is continuous function at
is continuous function at 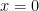 , then:
, then:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
7. Let  , where
, where  and
and  for all
for all  . Then the value of
. Then the value of 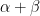 is:
is:
(A) 3
(B) 2
(C) -3
(D) 6
Click to View Answer
Correct Answer: [Insert Correct Option]
8. Range of ![y = \cos^{-1} \sqrt{\log_{[x]} \dfrac{[x]}{x}}](https://s0.wp.com/latex.php?latex=y+%3D+%5Ccos%5E%7B-1%7D+%5Csqrt%7B%5Clog_%7B%5Bx%5D%7D+%5Cdfrac%7B%5Bx%5D%7D%7Bx%7D%7D&bg=ffffff&fg=000&s=0&c=20201002) , (where
, (where ![[x]](https://s0.wp.com/latex.php?latex=%5Bx%5D&bg=ffffff&fg=000&s=0&c=20201002) denotes greatest integer less than or equal to
denotes greatest integer less than or equal to  )
)
(A) ![[0, \pi]](https://s0.wp.com/latex.php?latex=%5B0%2C+%5Cpi%5D&bg=ffffff&fg=000&s=0&c=20201002)
(B) ![[-1, 1]](https://s0.wp.com/latex.php?latex=%5B-1%2C+1%5D&bg=ffffff&fg=000&s=0&c=20201002)
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
9. Let  . If
. If  and
and 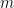 are the greatest and least value of
are the greatest and least value of 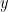 for all
for all  , then
, then  is equal to:
is equal to:
(A) 
(B) 
(C) 1
(D) None
Click to View Answer
Correct Answer: [Insert Correct Option]
10. If  and
and  , then standard deviation of observations
, then standard deviation of observations  and
and  is equal to:
is equal to:
(A) 8
(B) 16
(C) 4
(D) 2
Click to View Answer
Correct Answer: [Insert Correct Option]
11. In a triangle 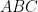 ,
,  . Then
. Then ![[a + b + c\sqrt{2}]](https://s0.wp.com/latex.php?latex=%5Ba+%2B+b+%2B+c%5Csqrt%7B2%7D%5D&bg=ffffff&fg=000&s=0&c=20201002) is equal to:
is equal to:
(A) 
(B) 
(C) 
(D) 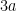
Click to View Answer
Correct Answer: [Insert Correct Option]
12.  equals:
equals:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
13. If  and roots
and roots  and
and  of equation
of equation  satisfy the condition
satisfy the condition  then
then  :
:
(A) -3
(B) -5
(C) -6
(D) -2
Click to View Answer
Correct Answer: [Insert Correct Option]
14. If the system of equation  ,
,  ,
,  is consistent then:
is consistent then:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
15. Let bag A contains 2 Red, 3 Green balls and bag B contains 3 Red, 2 Green balls. If two balls are drawn randomly from each of bag A & B and then put in to empty bag C. It is found that bag C contains equal number of red and green balls, then probability that 2 Red balls were drawn from bag B is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
16. Let  and
and  . Let
. Let  be a complex number such that
be a complex number such that  , then
, then  satisfies:
satisfies:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
17. Consider a circle 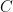 which touches the
which touches the 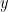 -axis at
-axis at  and cuts off an intercept
and cuts off an intercept  on the
on the  -axis. Then the radius of the circle
-axis. Then the radius of the circle 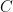 is equal to:
is equal to:
(A) 
(B) 9
(C) 8
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
18. A hyperbola passes through the foci of the ellipse  and its transverse and conjugate axes coincide with major and minor axes of the ellipse, respectively. If the product of their eccentricities in one, then the equation of the hyperbola is:
and its transverse and conjugate axes coincide with major and minor axes of the ellipse, respectively. If the product of their eccentricities in one, then the equation of the hyperbola is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
19. Let  and
and  . If
. If  ,
,  and
and  ,
, 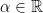 , then the value of
, then the value of  is equal to:
is equal to:
(A) 9
(B) 15
(C) 13
(D) 11
Click to View Answer
Correct Answer: [Insert Correct Option]
20. If the shortest distance between the lines  and
and  ,
, 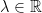 is
is  , then the integral value of
, then the integral value of  is equal to:
is equal to:
(A) 3
(B) 2
(C) 5
(D) -1
Click to View Answer
Correct Answer: [Insert Correct Option]
SECTION B: Numerical Value Type Questions
21. If the value of  is
is  (
( ) Find
) Find 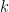 .
.
Click to View Answer
Correct Answer: [Insert Integer Value]
22. If  , then value of
, then value of  is:
is:
Click to View Answer
Correct Answer: [Insert Integer Value]
23. The minimum value of the expression  for
for  is:
is:
Click to View Answer
Correct Answer: [Insert Integer Value]
24. Number of five digit natural numbers, with sum of digits equal to 43 are:
Click to View Answer
Correct Answer: [Insert Integer Value]
25. Let the points of intersections of the lines  ,
,  and
and  are the mid points of the sides of a triangle
are the mid points of the sides of a triangle 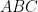 . Then the area of the triangle
. Then the area of the triangle 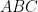 is:
is:
Click to View Answer
Correct Answer: [Insert Integer Value]
