Mathematics Questions
1. A square matrix  satisfies
satisfies  . If
. If  , then
, then  is:
is:
(A) 4
(B) 5
(C) 6
(D) 7
Click to View Answer
Correct Answer: [Insert Correct Option]
2. Let  and
and  . Then the value of
. Then the value of  is:
is:
(A) 2
(B) 1
(C) 4
(D) None of these
Click to View Answer
Correct Answer: [Insert Correct Option]
3. Let  and
and  be
be  matrices such that
matrices such that  , then:
, then:
(A) 
(B) 
(C) 
(D) None of these
Click to View Answer
Correct Answer: [Insert Correct Option]
4. If 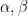 are the roots of the equation
are the roots of the equation  and
and  , then:
, then:
(A)  is an involutory matrix
is an involutory matrix
(B)  is a singular matrix
is a singular matrix
(C) 
(D) None of these
Click to View Answer
Correct Answer: [Insert Correct Option]
5. Consider the parabola  . Then:
. Then:
| Column-I | Column-II |
|---|---|
| (A) Vertex | (P) |
| (B) Focus | (Q) |
| (C) End of Latus Rectum | (R) |
| (D) Point of intersection directrix and axis | (S) |
(A) A-P, B-Q, C-R, D-S
(B) A-S, B-R, C-Q, D-P
(C) A-R, B-S, C-P, D-Q
(D) A-S, B-P, C-Q, D-R
Click to View Answer
Correct Answer: [Insert Correct Option]
6. If the eccentricity of the hyperbola  is
is 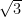 times the eccentricity of the ellipse
times the eccentricity of the ellipse  , then the value of
, then the value of 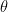 equals:
equals:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
7. The coordinates of a point on the parabola  whose focal distance is 4 are:
whose focal distance is 4 are:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
8. The eccentricity of the hyperbola with asymptotes  and
and  is:
is:
(A) 2
(B) 
(C) 
(D) 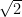
Click to View Answer
Correct Answer: [Insert Correct Option]
9. Minimum distance between the parabola  and its image with respect to the line
and its image with respect to the line  is:
is:
(A) 
(B) 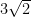
(C) 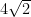
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
10. If the line  is a chord of the parabola
is a chord of the parabola  , then its length is:
, then its length is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
11. The axis of a parabola lies along the  -axis. If its vertex and focus are at distances 2 and 4 respectively from the origin, on the positive
-axis. If its vertex and focus are at distances 2 and 4 respectively from the origin, on the positive  -axis, then which of the following points does not lie on it?
-axis, then which of the following points does not lie on it?
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
12. If the area of the triangle whose one vertex is at the vertex of the parabola  and the other two vertices are the points of intersection of the parabola and the
and the other two vertices are the points of intersection of the parabola and the 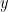 -axis is 250 sq. units, then a value of ‘
-axis is 250 sq. units, then a value of ‘ ‘ is:
‘ is:
(A) 
(B) 
(C) 
(D) 5
Click to View Answer
Correct Answer: [Insert Correct Option]
13. A ray of light moving parallel to the  -axis gets reflected from a parabolic mirror whose equation is
-axis gets reflected from a parabolic mirror whose equation is  . After reflection, the ray must pass through the point:
. After reflection, the ray must pass through the point:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
14. Value of ‘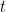 ‘ for which the intercept cut off by the chord
‘ for which the intercept cut off by the chord  of the parabola
of the parabola  subtends a right angle at its vertex is:
subtends a right angle at its vertex is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
15. The ellipse  is inscribed in a rectangle aligned with the coordinate axes, which in turn is inscribed in another ellipse that passes through the point
is inscribed in a rectangle aligned with the coordinate axes, which in turn is inscribed in another ellipse that passes through the point 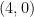 . Then the equation of the ellipse is:
. Then the equation of the ellipse is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
16. Planet  orbits around its sun,
orbits around its sun,  , in an elliptical orbit with the sun at one of the foci. When
, in an elliptical orbit with the sun at one of the foci. When  is closest to
is closest to  , it is 2 units away. When
, it is 2 units away. When  is farthest from
is farthest from  , it is 18 units away. Then the equation of motion of planet
, it is 18 units away. Then the equation of motion of planet  around its sun
around its sun  , assuming
, assuming  is at the center of the coordinate plane and the other focus lies on the negative
is at the center of the coordinate plane and the other focus lies on the negative 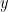 -axis, is:
-axis, is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
17. A man running around a racecourse notes that the sum of the distances of two flag-posts from him is always 10 meters and the distance between the flag-posts is 8 meters. The area of the path he encloses in square meters is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
18. If the area of the auxiliary circle of the ellipse  (
(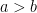 ) is twice the area of the ellipse, then the eccentricity of the ellipse is:
) is twice the area of the ellipse, then the eccentricity of the ellipse is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
19. The product of the lengths of perpendiculars drawn from any point on the hyperbola  to its asymptotes is:
to its asymptotes is:
(A) 
(B) 
(C) 
(D) 2
Click to View Answer
Correct Answer: [Insert Correct Option]
20. The foci of the ellipse  and those of the hyperbola
and those of the hyperbola  coincide, then
coincide, then 
(A) 3
(B) 7
(C) 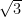
(D) 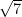
Click to View Answer
Correct Answer: [Insert Correct Option]
21. If matrix ![A = [a_{ij}]_{3 \times 3}](https://s0.wp.com/latex.php?latex=A+%3D+%5Ba_%7Bij%7D%5D_%7B3+%5Ctimes+3%7D&bg=ffffff&fg=000&s=0&c=20201002) and
and  and element
and element  , then the number of matrices
, then the number of matrices  is equal to:
is equal to:
Click to View Answer
Correct Answer: [Insert Correct Answer]
22. Let  and
and  be two non-singular matrices of order 3 such that
be two non-singular matrices of order 3 such that  and
and  , then
, then  is (where
is (where  is the adjoint of matrix
is the adjoint of matrix  ):
):
Click to View Answer
Correct Answer: [Insert Correct Answer]
23. If the line  is a focal chord of the parabola
is a focal chord of the parabola  , then the value of
, then the value of  is:
is:
Click to View Answer
Correct Answer: [Insert Correct Answer]
24. The radius of the largest circle that passes through the focus of the parabola  and is contained in it is:
and is contained in it is:
Click to View Answer
Correct Answer: [Insert Correct Answer]
25. The radius of the circle passing through the foci of the ellipse  and having its center at
and having its center at  is:
is:
Click to View Answer
Correct Answer: [Insert Correct Answer]
26. A point  on the ellipse
on the ellipse  has the eccentric angle
has the eccentric angle  . The sum of the distances of
. The sum of the distances of  from the two foci is:
from the two foci is:
Click to View Answer
Correct Answer: [Insert Correct Answer]
27. The focal length of the hyperbola  is:
is:
Click to View Answer
Correct Answer: [Insert Correct Answer]
28. A hyperbola is such that its length of latus rectum equals 6 and the length of its conjugate axis is equal to one third of its distance between foci. If its eccentricity is  (where
(where  and
and 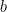 are prime), then the value of
are prime), then the value of 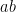 is:
is:
Click to View Answer
Correct Answer: [Insert Correct Answer]
29. If the equations of the directrices of the hyperbola  are
are 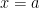 and
and  , then the value of
, then the value of  is:
is:
Click to View Answer
Correct Answer: [Insert Correct Answer]
30. Let 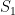 and
and 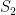 be the foci of the hyperbola
be the foci of the hyperbola  ,
,  . If
. If  is a variable point on the hyperbola, then the minimum value of
is a variable point on the hyperbola, then the minimum value of  is:
is:
Click to View Answer
Correct Answer: [Insert Correct Answer]
