SECTION A: Multiple Choice Questions
1. Consider a sequence of 101 terms as
 If the
If the  term is the greatest term of the sequence, then
term is the greatest term of the sequence, then  is equal to:
is equal to:
(A) 48
(B) 49
(C) 50
(D) 51
Click to View Answer
Correct Answer: [Insert Correct Option]
2. Number of rational terms in the binomial expansion of  is:
is:
(A) 7
(B) 8
(C) 9
(D) 10
Click to View Answer
Correct Answer: [Insert Correct Option]
3. If  , then
, then  is equal to:
is equal to:
(A) 0
(B) 
(C) 1
(D) -1
Click to View Answer
Correct Answer: [Insert Correct Option]
4. The coefficient of  in the expansion of
in the expansion of  is:
is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
5. Sum of all the rational terms in the expansion  is:
is:
(A) 27
(B) 256
(C) 283
(D) None of these
Click to View Answer
Correct Answer: [Insert Correct Option]
6. Find the remainder when  (24 times 5) is divided by 24:
(24 times 5) is divided by 24:
(A) 5
(B) 21
(C) 10
(D) 0
Click to View Answer
Correct Answer: [Insert Correct Option]
7.  , and
, and  , when divided by 4, leave remainders of 0, 1, and 2 respectively. Find the number of nonnegative integer solutions of the equation
, when divided by 4, leave remainders of 0, 1, and 2 respectively. Find the number of nonnegative integer solutions of the equation  :
:
(A) 45
(B) 55
(C) 105
(D) 190
Click to View Answer
Correct Answer: [Insert Correct Option]
8. If matrix ![A = [a_{ij}]_{3 \times 3}](https://s0.wp.com/latex.php?latex=A+%3D+%5Ba_%7Bij%7D%5D_%7B3+%5Ctimes+3%7D&bg=ffffff&fg=000&s=0&c=20201002) and
and  and element
and element  , then the number of matrices
, then the number of matrices  is equal to:
is equal to:
(A) 3375
(B) 2744
(C) 6750
(D) 5488
Click to View Answer
Correct Answer: [Insert Correct Option]
9. How many words can be made by using all letters of the word ‘BAHUBALI’ if all words start and end with vowels?
(A) 2160
(B) 900
(C) 1560
(D) 780
Click to View Answer
Correct Answer: [Insert Correct Option]
10. If the coefficient of  in the expansion of
in the expansion of  is
is  , then
, then 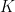 is equal to:
is equal to:
(A) 215
(B) 315
(C) 210
(D) None
Click to View Answer
Correct Answer: [Insert Correct Option]
11. In a circle, 20 persons are seated. Then the number of ways of selecting 5 persons such that no two persons are consecutive is:
(A) 
(B) 
(C) 
(D) None
Click to View Answer
Correct Answer: [Insert Correct Option]
12. How many six-digit numbers are there in which no digit is repeated, even digits appear at even places, odd digits appear at odd places, and the number is divisible by 4?
(A) 3600
(B) 2700
(C) 2160
(D) 1440
Click to View Answer
Correct Answer: [Insert Correct Option]
13. Number of integer solutions of  :
:
(A) 800
(B) 12800
(C) 6400
(D) 3200
Click to View Answer
Correct Answer: [Insert Correct Option]
14. If a vector  of magnitude
of magnitude  is directed along the bisector of the angle between the vectors
is directed along the bisector of the angle between the vectors  and
and  , then
, then  is:
is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
15. The set of values of  for which the angle between the vectors
for which the angle between the vectors  and
and  is acute for every
is acute for every  is:
is:
(A) 
(B) ![[0, 4/3]](https://s0.wp.com/latex.php?latex=%5B0%2C+4%2F3%5D&bg=ffffff&fg=000&s=0&c=20201002)
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
16. A unit vector which is perpendicular to the vector  and is coplanar with the vectors
and is coplanar with the vectors  and
and  is:
is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
17. Let 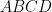 be a parallelogram such that
be a parallelogram such that  ,
,  , and
, and  is an acute angle. If
is an acute angle. If  is the vector that coincides with the altitude directed from the vertex
is the vector that coincides with the altitude directed from the vertex  to the side
to the side  , then
, then  is given by:
is given by:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
18. The vector  is rotated through an angle
is rotated through an angle 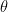 and doubled in magnitude, then it becomes
and doubled in magnitude, then it becomes  . The values of
. The values of  are:
are:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
19. If 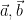 , and
, and  are unit vectors, then
are unit vectors, then  does not exceed:
does not exceed:
(A) 4
(B) 9
(C) 8
(D) 6
Click to View Answer
Correct Answer: [Insert Correct Option]
20. Let  be the equation of an ellipse in the
be the equation of an ellipse in the  –
–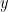 plane.
plane.  and
and  are two points whose position vectors are
are two points whose position vectors are  and
and  . Then the position vector of a point
. Then the position vector of a point  on the ellipse such that
on the ellipse such that  is:
is:
(A) 
(B) 
(C) 
(D) None of these
Click to View Answer
Correct Answer: [Insert Correct Option]
21. The number of values of ‘ ‘ for which the fourth term in the expansion
‘ for which the fourth term in the expansion  is 336 is:
is 336 is:
Click to View Answer
Correct Answer: [Insert Correct Answer]
22. The  term in the expansion of
term in the expansion of  is independent of
is independent of  , then the sum of the divisors of
, then the sum of the divisors of  is:
is:
Click to View Answer
Correct Answer: [Insert Correct Answer]
23. If  is divided by 11, then the remainder is:
is divided by 11, then the remainder is:
Click to View Answer
Correct Answer: [Insert Correct Answer]
24. The number of shortest paths from  to
to  , which are neither passing through
, which are neither passing through  nor
nor 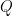 nor
nor  nor
nor  , is:
, is:
Click to View Answer
Correct Answer: [Insert Correct Answer]
25. The total number of two-digit numbers ‘ ‘ such that
‘ such that  is a multiple of 10 is:
is a multiple of 10 is:
Click to View Answer
Correct Answer: [Insert Correct Answer]
26. 20 persons are sitting in a particular arrangement around a circular table. Three persons are to be selected for leaders. The number of ways of selecting three persons such that no two were sitting adjacent to each other is:
Click to View Answer
Correct Answer: [Insert Correct Answer]
27. The maximum number of points of intersection of five lines and four circles is (if no two of them are similar):
[Image of intersecting lines and circles]
Click to View Answer
Correct Answer: [Insert Correct Answer]
28. Consider the set of eight vectors  . Three non-coplanar vectors can be chosen from
. Three non-coplanar vectors can be chosen from 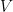 in
in  ways. Then
ways. Then  is:
is:
Click to View Answer
Correct Answer: [Insert Correct Answer]
29. If  ,
,  , and
, and  , then the magnitude of the projection of
, then the magnitude of the projection of  on
on  is:
is:
Click to View Answer
Correct Answer: [Insert Correct Answer]
30. If vectors  satisfy the condition
satisfy the condition  , then
, then  is equal to:
is equal to:
Click to View Answer
Correct Answer: [Insert Correct Answer]
