SECTION A: Multiple Choice Questions
1. Let  and
and  . Let
. Let  be a complex number such that
be a complex number such that  , then
, then  satisfies:
satisfies:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
2. If  ,
,  ,
,  , and
, and  , then
, then 
(A) 2
(B) 3
(C) 4
(D) 6
Click to View Answer
Correct Answer: [Insert Correct Option]
3. If  , then the locus of
, then the locus of 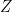 will be:
will be:
(A) Straight line
(B) Circle
(C) Parabola
(D) Ellipse
Click to View Answer
Correct Answer: [Insert Correct Option]
4. Eccentricity of the given curve is: If  .
.
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
5. If  are complex numbers such that
are complex numbers such that  ,
,  ,
,  , then the maximum value of
, then the maximum value of  is:
is:
(A) 87
(B) 79
(C) 52
(D) None
Click to View Answer
Correct Answer: [Insert Correct Option]
6. If  , then the value of
, then the value of  is:
is:
(A) 0
(B) 1
(C) 2
(D) 3
Click to View Answer
Correct Answer: [Insert Correct Option]
7. If  are complex numbers such that
are complex numbers such that  ,
,  , and
, and  , then
, then 
(A) 
(B) 
(C) 
(D) 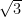
Click to View Answer
Correct Answer: [Insert Correct Option]
8. If  , then:
, then:
(A)  ,
, 
(B)  ,
, 
(C)  ,
, 
(D)  ,
, 
Click to View Answer
Correct Answer: [Insert Correct Option]
9. If  and
and  , then
, then  is:
is:
(A) 3
(B) 1
(C) 2
(D) 4
Click to View Answer
Correct Answer: [Insert Correct Option]
10. If  ,
,  , and
, and
 , then:
, then:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
11. If 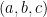 is the image of the point
is the image of the point  in the line
in the line  , then
, then  is equal to:
is equal to:
(A) -1
(B) 2
(C) 3
(D) 4
Click to View Answer
Correct Answer: [Insert Correct Option]
12. The lines  and
and  ,
,  , are coplanar if:
, are coplanar if:
(A) 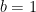 ,
, 
(B)  ,
, 
(C)  ,
, 
(D)  ,
, 
Click to View Answer
Correct Answer: [Insert Correct Option]
13. If the shortest distance between the lines  and
and  is
is  , then the sum of all possible values of
, then the sum of all possible values of  is:
is:
(A) 16
(B) 6
(C) 12
(D) 15
Click to View Answer
Correct Answer: [Insert Correct Option]
14. The equation of the line through the point  and perpendicular to the line
and perpendicular to the line  is:
is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
15. Let 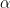 be the angle between the lines whose direction cosines satisfy the equations
be the angle between the lines whose direction cosines satisfy the equations  and
and  . Then the value of
. Then the value of  is:
is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
16. If the foot of the perpendicular from point  on the line
on the line  ,
,  , is
, is  , then the shortest distance between the line
, then the shortest distance between the line  and line
and line  is equal to:
is equal to:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
17. Let the position vectors of two points 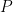 and
and 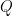 be
be  and
and  , respectively. Let
, respectively. Let 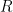 and
and  be two points such that the direction ratios of lines
be two points such that the direction ratios of lines 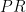 and
and  are
are  and
and  , respectively. Let lines
, respectively. Let lines 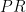 and
and  intersect at
intersect at 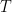 . If the vector
. If the vector  is perpendicular to both
is perpendicular to both  and
and  and the length of vector
and the length of vector  is
is 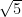 units, then the modulus of a position vector of
units, then the modulus of a position vector of 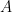 is:
is:
(A) 
(B) 
(C) 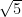
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
18. If the two lines  ,
,  and
and  are perpendicular, then an angle between the lines
are perpendicular, then an angle between the lines 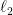 and
and  is:
is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
19. If two straight lines whose direction cosines are given by the relations  ,
,  are parallel, then the positive value of
are parallel, then the positive value of  is:
is:
(A) 6
(B) 4
(C) 3
(D) 2
Click to View Answer
Correct Answer: [Insert Correct Option]
20. If the length of the perpendicular drawn from the point  ,
, 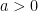 , on the line
, on the line  is
is  units and
units and  is the image of the point
is the image of the point 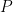 in this line, then
in this line, then  is equal to:
is equal to:
(A) 7
(B) 8
(C) 12
(D) 14
Click to View Answer
Correct Answer: [Insert Correct Option]
21. Let  ,
,  , then the least value of
, then the least value of
 is:
is:
Click to View Answer
Correct Answer: [Insert Correct Answer]
22. If  , then
, then  is equal to?
is equal to?
Click to View Answer
Correct Answer: [Insert Correct Answer]
23. Value of  is equal to:
is equal to:
Click to View Answer
Correct Answer: [Insert Correct Answer]
24. If the shortest distance between the lines  and
and  is 9, then
is 9, then 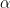 is equal to:
is equal to:
Click to View Answer
Correct Answer: [Insert Correct Answer]
25. Let  . If the mirror image of the point
. If the mirror image of the point  with respect to the line
with respect to the line  is
is  , then
, then  is equal to:
is equal to:
Click to View Answer
Correct Answer: [Insert Correct Answer]
