Mathematics Questions (Continued)
1. The relation  on the set
on the set  is:
is:
(A) Reflexive, Symmetric but not Transitive
(B) Reflexive, Transitive but not Symmetric
(C) Symmetric, Transitive but not Reflexive
(D) Equivalence relation
Click to View Answer
Correct Answer: [Insert Correct Option]
2. A relation on the set  , where
, where 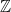 is the set of integers, is defined by
is the set of integers, is defined by  . Then the number of elements in the power set of
. Then the number of elements in the power set of  is:
is:
(A) 32
(B) 64
(C) 16
(D) 8
Click to View Answer
Correct Answer: [Insert Correct Option]
3. Let  be a relation on
be a relation on 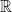 , given by
, given by  . Then
. Then  is:
is:
(A) Reflexive but neither symmetric nor transitive
(B) Reflexive and transitive but not symmetric
(C) Reflexive and symmetric but not transitive
(D) An equivalence relation
Click to View Answer
Correct Answer: [Insert Correct Option]
4. Let the mean and variance of 12 observations be  and 4 respectively. Later on, it was observed that two observations were considered as 9 and 10 instead of 7 and 14 respectively. If the correct variance is
and 4 respectively. Later on, it was observed that two observations were considered as 9 and 10 instead of 7 and 14 respectively. If the correct variance is  , where
, where  and
and  are coprime, then
are coprime, then  is equal to:
is equal to:
(A) 316
(B) 314
(C) 317
(D) 315
Click to View Answer
Correct Answer: [Insert Correct Option]
5. The mean and variance of a binomial distribution are  and
and  respectively. If
respectively. If  , then
, then  is equal to:
is equal to:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
6. Find the M.D. about median for the following data:
| 3 | 9 | 17 | 23 | 27 | |
| 8 | 10 | 12 | 9 | 5 |
(A) 8
(B) 6.72
(C) 17
(D) 9.81
Click to View Answer
Correct Answer: [Insert Correct Option]
7. The mean of five numbers is 0 and their variance is 2. If three of those numbers are  , and 2, then the other two numbers are:
, and 2, then the other two numbers are:
(A) 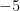 and 3
and 3
(B)  and 2
and 2
(C)  and 1
and 1
(D) 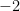 and 0
and 0
Click to View Answer
Correct Answer: [Insert Correct Option]
8. The standard deviation for the scores  , and 7 is 2. Then the standard deviation of
, and 7 is 2. Then the standard deviation of  , and 78 is:
, and 78 is:
(A) 2
(B) 4
(C) 22
(D) 11
Click to View Answer
Correct Answer: [Insert Correct Option]
9. The mean marks obtained by 300 students in Mathematics are 45. The mean of the top 100 students was 70 and the mean of the last 100 was 20. Then the mean of the remaining 100 students is:
(A) 40
(B) 50
(C) 45
(D) 43
Click to View Answer
Correct Answer: [Insert Correct Option]
10. There are 100 families in a society: 40 families buy newspaper A, 30 families buy newspaper B, 30 families buy newspaper C, 10 families buy newspapers A and B, 8 families buy newspapers B and C, 5 families buy newspapers A and C, and 3 families buy newspapers A, B, and C. Then the number of families who do not buy any newspaper is:
[Image of Venn diagram 3 sets]
(A) 20
(B) 80
(C) 0
(D) None of these
Click to View Answer
Correct Answer: [Insert Correct Option]
11. 5 different balls are placed in 5 different boxes randomly. Find the probability that exactly two boxes remain empty. Given each box can hold any number of balls:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
12. A fair die is thrown up to 20 times. The probability that on the 10th throw, the fourth six appears is:
(A) 
(B) 
(C) 
(D) None
Click to View Answer
Correct Answer: [Insert Correct Option]
13. The chances of defective screws in three boxes A, B, C are  ,
,  ,
,  respectively. One box is selected at random and a screw drawn from it at random is found to be defective. Then the probability that it came from box A is:
respectively. One box is selected at random and a screw drawn from it at random is found to be defective. Then the probability that it came from box A is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
14. There are 10 stations between two cities A and B. A train is to stop at three of these 10 stations. The probability that no two of these three stations are consecutive is:
(A) 
(B) 
(C) 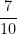
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
15. A seven-digit number is formed using digits 3, 3, 4, 4, 4, 5, 5. The probability that the number so formed is divisible by 2 is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
16. If two events  and
and  are such that
are such that  ,
,  , and
, and  , then the value of
, then the value of ![P\left[ \dfrac{B}{A \cup B^C} \right]](https://s0.wp.com/latex.php?latex=P%5Cleft%5B+%5Cdfrac%7BB%7D%7BA+%5Ccup+B%5EC%7D+%5Cright%5D&bg=ffffff&fg=000&s=0&c=20201002) is equal to:
is equal to:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
17. If the probability of A failing an examination is  and that of B is
and that of B is  , then the probability that either A or B fails is:
, then the probability that either A or B fails is:
(A) 
(B) 
(C) 
(D) None of these
Click to View Answer
Correct Answer: [Insert Correct Option]
18. Sixteen players  play in a tournament. If they are grouped into eight pairs, then the probability that
play in a tournament. If they are grouped into eight pairs, then the probability that  and
and  are in different groups is equal to:
are in different groups is equal to:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
19. Two dice are thrown together. The probability that the sum of the numbers appearing on them is 9, given that the number 5 always occurs on the first die, is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
20. For 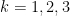 , the box
, the box  contains
contains 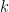 red balls and
red balls and  white balls. Let
white balls. Let  ,
,  , and
, and  , where
, where  represents the probability of selecting box
represents the probability of selecting box  . A box is selected randomly and a ball is drawn. If it is known that the drawn ball is red, then the probability that it has come from box
. A box is selected randomly and a ball is drawn. If it is known that the drawn ball is red, then the probability that it has come from box  is:
is:
(A) 
(B) 
(C) 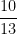
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
21. Total number of equivalence relations defined in the set  is:
is:
Click to View Answer
Correct Answer: [Insert Correct Answer]
22. Given the relation  on the set
on the set  , the minimum number of ordered pairs which, when added to
, the minimum number of ordered pairs which, when added to  , make it an equivalence relation is:
, make it an equivalence relation is:
Click to View Answer
Correct Answer: [Insert Correct Answer]
23. Number of ways in which 4 people can be selected out of 10 people sitting in a row such that exactly two are consecutive?
Click to View Answer
Correct Answer: [Insert Correct Answer]
24. There are 100 tickets numbered  . One ticket is selected at random. Suppose
. One ticket is selected at random. Suppose  and
and  are the sum and product of the digits of the number found on the ticket, and
are the sum and product of the digits of the number found on the ticket, and  , then
, then 
Click to View Answer
Correct Answer: [Insert Correct Answer]
25. A die is thrown 31 times. If the probability of getting 2, 4, or 5 at most 15 times is  , then
, then 
Click to View Answer
Correct Answer: [Insert Correct Answer]
