Mathematics Questions
1. Two circles of radii ‘ ‘ and ‘
‘ and ‘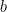 ‘ touching each other externally are inscribed in the area bounded by
‘ touching each other externally are inscribed in the area bounded by  and the
and the  -axis. If
-axis. If  , then
, then  is equal to:
is equal to:
(A) 1
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
2. If the lines  and
and  are two normals of a circle passing through
are two normals of a circle passing through  , then the equation of the circle is:
, then the equation of the circle is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
3. The image of the circle  with respect to the line
with respect to the line  is:
is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
4. Let  be the region satisfying
be the region satisfying  ,
,  . Then the area of
. Then the area of  is:
is:
(A) 
(B) 
(C) 
(D) 2
Click to View Answer
Correct Answer: [Insert Correct Option]
5. The population  at time
at time 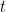 of a certain mouse species satisfies the differential equation
of a certain mouse species satisfies the differential equation  . If
. If  , then the time at which the population becomes zero is:
, then the time at which the population becomes zero is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
6. Let  be a solution of
be a solution of  . If
. If  , then
, then  equals:
equals:
(A) 2
(B) 
(C) 
(D) 3
Click to View Answer
Correct Answer: [Insert Correct Option]
7. The equation of the auxiliary circle of the ellipse which passes through  and has foci
and has foci  and
and  is:
is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
8.  ,
,  , and
, and 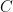 are points on the parabola
are points on the parabola  such that
such that  . Then the least positive value of the ordinate of
. Then the least positive value of the ordinate of 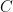 is:
is:
(A) 3
(B) 4
(C) 1
(D) 2
Click to View Answer
Correct Answer: [Insert Correct Option]
9. If 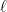 is the length of the latus rectum of the parabola
is the length of the latus rectum of the parabola  , then
, then 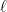 equals:
equals:
(A) 5
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
10. A square matrix  of order 3 satisfies
of order 3 satisfies  , where
, where 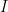 is an identity matrix of order 3. If
is an identity matrix of order 3. If  , then
, then  is equal to:
is equal to:
(A) 4
(B) 5
(C) 6
(D) 7
Click to View Answer
Correct Answer: [Insert Correct Option]
11. Let  ,
,  , and
, and  . If
. If  , then
, then  is (where
is (where 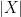 ,
,  , and
, and  denote determinant value, trace, and adjoint of matrix
denote determinant value, trace, and adjoint of matrix 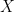 respectively):
respectively):
(A) 5
(B) 12
(C) 30
(D) 60
Click to View Answer
Correct Answer: [Insert Correct Option]
12. If  and
and  are two complex numbers satisfying
are two complex numbers satisfying  and
and  , then the maximum value of
, then the maximum value of  is:
is:
(A) 14
(B) 15
(C) 33
(D) 31
Click to View Answer
Correct Answer: [Insert Correct Option]
13. If  and
and  are conjugate complex numbers and
are conjugate complex numbers and  , then
, then  is equal to:
is equal to:
(A) 4
(B) 5
(C) 6
(D) 7
Click to View Answer
Correct Answer: [Insert Correct Option]
14. The image of the line  in the plane
in the plane  is the line:
is the line:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
15. Vector equation of the line passing through  and perpendicular to the lines
and perpendicular to the lines  and
and  is:
is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
16. Let  be a relation defined as
be a relation defined as  if
if  . Then, the relation
. Then, the relation  is (
is ( ):
):
(A) Reflexive
(B) Not symmetric
(C) Transitive
(D) None of these
Click to View Answer
Correct Answer: [Insert Correct Option]
17. If the mean of a set of  numbers
numbers  is
is  , then the mean of the numbers
, then the mean of the numbers  ,
,  , will be:
, will be:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
18. The variance of the observations  is:
is:
(A) 21
(B) 21.2
(C) 21.4
(D) None of these
Click to View Answer
Correct Answer: [Insert Correct Option]
19. A box contains 20 identical balls of which 5 are white and 15 are black. The balls are drawn at random from the box one at a time with replacement. The probability that a white ball is drawn for the  time on the
time on the  draw is:
draw is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
20. If  and
and  are two events such that
are two events such that  , then
, then  is equal to:
is equal to:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Option]
21. If  is the slope of the common tangent of the parabola
is the slope of the common tangent of the parabola  and the circle
and the circle  , then
, then  is equal to:
[Image showing the common tangent to the parabola y^2 = 16x and the circle x^2 + y^2 = 8]
is equal to:
[Image showing the common tangent to the parabola y^2 = 16x and the circle x^2 + y^2 = 8]
Click to View Answer
Correct Answer: [Insert Correct Answer]
22. Given  is a square matrix of order 3, such that
is a square matrix of order 3, such that  and
and  is
is  , then
, then  is:
is:
Click to View Answer
Correct Answer: [Insert Correct Answer]
23. 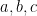 are three complex numbers on the unit circle
are three complex numbers on the unit circle  such that
such that  , then
, then  is equal to:
is equal to:
Click to View Answer
Correct Answer: [Insert Correct Answer]
24. If  is the minimum distance between the lines
is the minimum distance between the lines  and
and  , then
, then  is equal to:
is equal to:
Click to View Answer
Correct Answer: [Insert Correct Answer]
25. There are 10 pairs of shoes in a cupboard, from which 4 shoes are picked at random. If  is the probability that there is at least one pair, find
is the probability that there is at least one pair, find  .
.
Click to View Answer
Correct Answer: [Insert Correct Answer]
