JEE MAIN TEST – 1 – JEE MATH APEX

SECTION A: Multiple Choice Questions

1. Let $A$ be the set of all real solutions of equation $x(x^2 + 3|x| + 5|x - 1| + 6|x - 2|) = 0$ and $B$ be the set of all real solutions of equation $x^2 - |x| - 12 = 0$ , then number of subsets of the set $A \times B$ is:

(A) 2

(B) 4

(D) 16

Click to View Answer

Correct Answer: [Insert Correct Answer]

2. Let $\alpha, \beta, \gamma$ be three roots of equation $x^3 + bx + c = 0$ such that $\beta \gamma = 1 = -\alpha$ . If $\alpha^n + \beta^n + \gamma^n = -3$ then value of $n$ can be:

(A) 9

(B) 8

(D) 6

Click to View Answer

Correct Answer: [Insert Correct Answer]

3. Assertion A: The number of ways in which 3 married couples with their 4 children can sit in a row such that no husband and wife are together, are $10! - 3 \cdot 9! + 3 \cdot 8! - 7!$ .
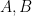Reason R: Number of ways of occurrence of at least one event out of three events $A, B$ & $C = n(A \cup B \cup C) = n(A) + n(B) + n(C) - n(A \cap B) - n(B \cap C) - n(C \cap A) + n(A \cap B \cap C)$ .

(A) Both A and R are correct but R is NOT the correct explanation of A

(B) Both A and R are correct and R is the correct explanation of A

(D) A is not correct but R is correct

Click to View Answer

Correct Answer: [Insert Correct Answer]

4. If for the complex number $z$ satisfying $|z - 2 - 2i| \leq 1$ , the maximum and minimum value of $|3iz + 6|$ is $M$ and $m$ then the value of $(M + m)$ is:

(A) 9

(B) 3

(D) 15

Click to View Answer

Correct Answer: [Insert Correct Answer]

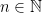5. If $2 \tan^2 \theta - 5 \sec \theta = 1$ has exactly 7 solutions in the interval $\left[0, \frac{n\pi}{2}\right]$ , then for the least value of $n \in \mathbb{N}$ value of $\sum_{k=1}^{n} \frac{k}{2^k}$ is equal to:

(A) $\frac{1}{2^{13}} (2^{14} - 15)$

(B) $1 - \frac{15}{2^{13}}$

(D) $\frac{1}{2^{14}} (2^{15} - 15)$

Click to View Answer

Correct Answer: [Insert Correct Answer]

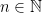6. Let the first term of the series be $a_1 = 6$ and its $r^{\text{th}}$ term be $a_r = 3 a_{r-1} + 6^r, \quad r = 2,3,\dots,n$ . For some $n \in \mathbb{N}$ , if the sum of the first $n$ terms of the series is $\frac{1}{5} (n^2 - 18n + 84) (4.6^n - 5.3^n + 1)$ , then $n$ is equal to:

(A) 9

(B) 6

(D) 8

Click to View Answer

Correct Answer: [Insert Correct Answer]

7. Consider the system of linear equations:
$2x + (p^2 - 2)y + 6z = 8$
$x + 2y + (q - 1)z = 5$
$x + y + 3z = 4, \quad \text{where } p, q \in \mathbb{R}.$
Which of the following statements is NOT TRUE?

(A) System will have a unique solution if $p \in \mathbb{R} - \{-2,2\}$ , $q \in \mathbb{R} - \{4\}$ .

(B) System is inconsistent if $p = 2$ , $q = 4$ .

(D) System is consistent if $p \in \mathbb{R}$ , $q \in \mathbb{R} - \{4\}$ .

Click to View Answer

Correct Answer: [Insert Correct Answer]

8. The value of $\int_{-\alpha}^{-1} \left( \sec^{-1} y - \tan^{-1} \sqrt{y^2 - 1} \right) dy + \int_{1}^{\alpha} \left( \sec^{-1} y - \tan^{-1} \sqrt{y^2 - 1} \right) dy$ (where $\alpha > 1$ and $\int_{1}^{\alpha} \sec^{-1} (y) dy = \beta$ ) is:

(A) $\pi (\alpha - 1) - \beta$

(B) $\pi \alpha - 2 \beta$

(D) $\pi (\alpha - 1) - 2 \beta$

Click to View Answer

Correct Answer: [Insert Correct Answer]

9. Match List-I with List-II and select the correct answer using the code given below the list.

List-I	List-II
(A) Let $(\vec{a} \times \vec{b}) \times \vec{c} = -5\vec{a} + 4\vec{b}$ and $\vec{a} \cdot \vec{b} = 3$ and $\vec{a} \times (\vec{b} \times \vec{c}) = \lambda \vec{b} + \mu \vec{c}$ , then $\|\lambda\| + \|\mu\|$ is	(I) 2
(B) If the line $y - \sqrt{3}x + 3 = 0$ cuts the parabola $y^2 = x + 2$ at A and B, given that $\|(PA)(PB)\| = \frac{\lambda_1 (2 + \sqrt{3})}{\lambda_2}$ , then $\frac{\lambda_1^2 + \lambda_2^2}{5}$ is	(II) 7
(C) The sum of all values of $x$ with $0 \leq x \leq 2\pi$ which satisfy $\sqrt{2} (\cos 2x - \sin x - 1) = 1 + 2 \sin x$ , is $k\pi$ , then $k$ is	(III) 6
(D) Value of $\int_{-\pi/4}^{\pi/4} \frac{x^9 - 3x^7 + x^5 + 1}{\cos^2 x} dx$ is	(IV) 5

(A) (A) – I, (B) – II, (C) – III, (D) – IV

(B) (A) – II, (B) – IV, (C) – III, (D) – I

(D) (A) – III, (B) – IV, (C) – II, (D) – I

Click to View Answer

Correct Answer: [Insert Correct Answer]

10. Let $y = y(x)$ be the solution of the differential equation $(\text{cosec} x) \mathrm{d}y + (2(1 - x) \cot x + x(x - 2)) \mathrm{d}x = 0$ such that $y\left(\frac{\pi}{2}\right) = 3$ . The value of $y(2)$ is equal to:

(A) 2

(B) $2(1 - \cos 2)$

(D) 3

Click to View Answer

Correct Answer: [Insert Correct Answer]

11. Consider the given data distribution. The mean deviation from median of given data is:

Class int.	0-6	6-12	12-18	18-24	24-30
Freq.	4	5	3	6	2

(A) 7

(B) 7.5

(D) 6.5

Click to View Answer

Correct Answer: [Insert Correct Answer]

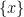12. Given a real valued function $f(x)$ defined as $f(x) = \begin{cases} \dfrac{\tan^2 \{x\}}{\{x\}^2} & ; x > 0 \\ 1 & ; x = 0 \\ \sqrt{\{x\}} \cot \{x\} & ; x < 0 \end{cases}$ where $\{x\}$ represent fractional part of $x$ . Then which of the following is INCORRECT:

(A) $\lim_{x \to 0^+} f(x) = 1$

(B) $\cot^{-1} \left( \lim_{x \to 0^-} f(x) \right)^2 = 1$

(D) $\lim_{x \to 0} f(x)$ exists.

Click to View Answer

Correct Answer: [Insert Correct Answer]

13. A square is inscribed in the circle $x^2 + y^2 - 10x - 6y + 30 = 0$ . One side of this square is parallel to $y = x + 3$ . If $(x_i, y_i)$ (where $i = 1, 2, 3, 4$ ) are the vertices of square then $\sum_{i=1}^{4} (x_i^2 + y_i^2)$ is equal to:

(A) 148

(B) 156

(D) 152

Click to View Answer

Correct Answer: [Insert Correct Answer]

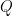14. Let $P$ be the point $(10, -2, -1)$ and $Q$ be the foot of the perpendicular drawn from the point $R(1, 7, 6)$ on the line passing through the points $(2, -5, 11)$ and $(-6, 7, -5)$ . Then the length of the line segment $PQ$ is equal to:

(A) 14

(B) 13

(D) 17

Click to View Answer

Correct Answer: [Insert Correct Answer]

15. Statement-1: If $a + b + c + d = 9$ and $a^2 + b^2 + c^2 + d^2 = 27$ , where $a, b, c, d$ are non-negative real numbers, then $d \in \left[0, \frac{9}{2}\right]$ .
Statement-2: $\left( \frac{a + b + c}{3} \right)^2 \leq \frac{a^2 + b^2 + c^2}{3}$ .

(A) Statement-1 is True, Statement-2 is True

(B) Statement-1 is False, Statement-2 is False

(D) Statement-1 is False, Statement-2 is True

Click to View Answer

Correct Answer: [Insert Correct Answer]

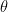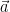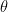16. Let unit vector $\vec{c}$ is inclined at an angle $\theta$ to a unit vector $\vec{a}$ and $\vec{b}$ which are perpendicular to each other. If $\vec{c} = \lambda (\vec{a} + \vec{b}) + \mu (\vec{a} \times \vec{b})$ where $\lambda, \mu$ be real, then $\theta$ belongs to:

(A) $\left( -\dfrac{\pi}{4}, 0 \right)$

(B) $\left[ 0, \dfrac{\pi}{4} \right]$

(D) $\left[ \dfrac{\pi}{4}, \dfrac{3\pi}{4} \right]$

Click to View Answer

Correct Answer: [Insert Correct Answer]

17. Length of focal chord of parabola $y^2 = 8x$ parallel to normal drawn to it at point with abscissa 2 is:

(A) 4

(B) 8

(D) 16

Click to View Answer

Correct Answer: [Insert Correct Answer]

18. Let $P$ be a relation defined on the set of interval $\left(0, \dfrac{\pi}{2}\right]$ such that $P = \{(a, b) : \text{cosec}^2 a - \cot^2 b = 1\}$ . Then $P$ is:

(A) Reflexive and symmetric but not transitive

(B) Reflexive and transitive but not symmetric

(D) Equivalence relation

Click to View Answer

Correct Answer: [Insert Correct Answer]

19. The area enclosed by $y = \ln x$ , $y = \ln|x|$ , $y = |\ln x|$ and $y = |\ln|x||$ is:

(A) 5

(B) 2

(D) 1

Click to View Answer

Correct Answer: [Insert Correct Answer]

20. Let $J = \int_{-5}^{-4} (3 - x^2) \tan (3 - x^2) \, \mathrm{d}x$ , $K = \int_{-2}^{-1} (6 - 6x + x^2) \tan (6x - x^2 - 6) \, \mathrm{d}x$ . Then $(J + K)$ :

(A) 0

(B) 1

(D) 3

Click to View Answer

Correct Answer: [Insert Correct Answer]

SECTION B: Numerical Value Type Questions

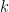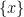21. The solution of the equation $\dfrac{8}{\{x\}} = \dfrac{9}{x} + \dfrac{10}{[x]}$ is of the form $\dfrac{k+1}{k}, k \in \mathbb{N}$ then $k$ is equal to (where $[x]$ denotes greatest integer less than $x$ & $\{x\}$ denotes fractional part of $x$ ):

Click to View Answer

Correct Answer: [Insert Integer Value]

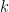22. If $\sum_{n=0}^{\infty} 2 \cot^{-1} \left( \dfrac{n^2 + n + 4}{2} \right) = k\pi$ , then the value of $k$ is:

Click to View Answer

Correct Answer: [Insert Integer Value]

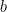23. If $a$ and $b$ are chosen randomly from the set $A = \{1, 2, 3, 4, 5, 6\}$ with replacement. If probability that $\lim_{x \to 0} \left( \dfrac{a^x + b^x}{2} \right)^{\dfrac{2}{x}} = 6$ is $\dfrac{p}{q}$ [ $H.C.F(p, q) = 1$ ] then $(q - p)$ is:

Click to View Answer

Correct Answer: [Insert Integer Value]

24. If $A = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}$ and $A^{2014} = \lambda A^{2013} + \mu A^{2012}$ then $(\lambda + \mu)$ is:

Click to View Answer

Correct Answer: [Insert Integer Value]

25. The coefficient of $x^{\dfrac{n^2 + n - 14}{2}}$ in $(x - 1)(x^2 - 2)(x^3 - 3) \ldots (x^n - n), n \geq 30$ is:

Click to View Answer

Correct Answer: [Insert Integer Value]