SECTION A: Multiple Choice Questions
1. Defining the set ![A = \{ \theta \in [0, 2\pi] :](https://s0.wp.com/latex.php?latex=A+%3D+%5C%7B+%5Ctheta+%5Cin+%5B0%2C+2%5Cpi%5D+%3A&bg=ffffff&fg=000&s=0&c=20201002)
 , then the sum
, then the sum  is equal to:
is equal to:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Answer]
2. If the locus of  such that
such that 
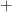
 , is a circle of radius
, is a circle of radius  and center
and center  , then
, then  is equal to:
is equal to:
(A) 16
(B) 24
(C) 12
(D) 18
Click to View Answer
Correct Answer: [Insert Correct Answer]
3. Among the statements:
(S1): The set contains exactly two elements, and
contains exactly two elements, and
(S2): The set contains infinitely many elements.
contains infinitely many elements.
(S1): The set
(S2): The set
(A) both are incorrect
(B) both are correct
(C) only (S2) is correct
(D) only (S1) is correct
Click to View Answer
Correct Answer: [Insert Correct Answer]
4. Let the product of  and
and  be
be  . Let
. Let 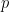 and
and  be the maximum and the minimum values of
be the maximum and the minimum values of  respectively. Then
respectively. Then  is equal to:
is equal to:
(A) 130
(B) 150
(C) 160
(D) 140
Click to View Answer
Correct Answer: [Insert Correct Answer]
5. If  are the vertices of an equilateral triangle, whose centroid is
are the vertices of an equilateral triangle, whose centroid is  , then
, then  is equal to:
is equal to:
(A) 0
(B) 1
(C) i
(D) -i
Click to View Answer
Correct Answer: [Insert Correct Answer]
6. Let  be such that
be such that  . Then the sum of all possible values of
. Then the sum of all possible values of 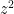 is :
is :
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Answer]
7. Let  be a complex number such that
be a complex number such that  . If
. If  ,
,  , then the maximum distance of
, then the maximum distance of  from the circle
from the circle  is :
is :
(A) 
(B) 3
(C) 
(D) 2
Click to View Answer
Correct Answer: [Insert Correct Answer]
8. Let  and
and  . Then the minimum value of
. Then the minimum value of  is :
is :
(A) 3
(B) 10
(C) 7
(D) 13
Click to View Answer
Correct Answer: [Insert Correct Answer]
9. If  and
and  are the roots of
are the roots of  , then
, then  is equal to:
is equal to:
(A) 2
(B) -6
(C) 6
(D) -2
Click to View Answer
Correct Answer: [Insert Correct Answer]
10. Let  be the origin, the point
be the origin, the point 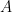 be
be  , the point
, the point  be such that
be such that  and
and  . Then
. Then
(A) area of triangle  is
is 
(B) area of triangle  is
is 
(C)  is a scalene triangle
is a scalene triangle
(D)  is an obtuse angled isosceles triangle
is an obtuse angled isosceles triangle
Click to View Answer
Correct Answer: [Insert Correct Answer]
11. If 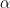 and
and 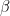 are the roots of the equation
are the roots of the equation  , where
, where  , then
, then
 is equal to:
is equal to:
(A) 441
(B) 312
(C) 409
(D) 398
Click to View Answer
Correct Answer: [Insert Correct Answer]
12. The number of complex numbers  satisfying
satisfying  and
and  , is :
, is :
(A) 8
(B) 10
(C) 4
(D) 6
Click to View Answer
Correct Answer: [Insert Correct Answer]
13. Let  , be the equation of a circle with center at
, be the equation of a circle with center at  . If the area of the triangle, whose vertices are at the points
. If the area of the triangle, whose vertices are at the points  and
and  is 11 square units, then
is 11 square units, then  equals:
equals:
(A) 
(B) 100
(C) 
(D) 50
Click to View Answer
Correct Answer: [Insert Correct Answer]
14. Let the curve  , divide the region
, divide the region  into two parts of areas
into two parts of areas 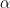 and
and 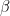 . Then
. Then  equals :
equals :
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Answer]
15. Let  and
and  be three complex numbers on the circle
be three complex numbers on the circle  with
with  ,
,  and
and  . If
. If  , then the value of
, then the value of  is :
is :
(A) 41
(B) 29
(C) 24
(D) 31
Click to View Answer
Correct Answer: [Insert Correct Answer]
16. Let  be a complex number such that the real part of
be a complex number such that the real part of  is zero. Then, the maximum value of
is zero. Then, the maximum value of  is equal to
is equal to
(A) 8
(B) 12
(C) 10
(D) 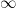
Click to View Answer
Correct Answer: [Insert Correct Answer]
17. The sum of all possible values of ![\theta \in[-\pi, 2 \pi]](https://s0.wp.com/latex.php?latex=%5Ctheta+%5Cin%5B-%5Cpi%2C+2+%5Cpi%5D+&bg=ffffff&fg=000&s=0&c=20201002) , for which
, for which  is purely imaginary, is equal to :
is purely imaginary, is equal to :
(A) 
(B) 
(C) 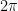
(D) 
Click to View Answer
Correct Answer: [Insert Correct Answer]
18. Let  be a complex number such that
be a complex number such that  and
and  . Then the value of
. Then the value of  is
is
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Answer]
19. If the set  has
has 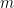 elements and
elements and  , where
, where  , then the value of
, then the value of  is
is
(A) 12
(B) 4
(C) 8
(D) 5
Click to View Answer
Correct Answer: [Insert Correct Answer]
