SECTION A: Quadratic Equations
1. The sum of the squares of the roots of  and the squares of the roots of
and the squares of the roots of  , is:
, is:
(A) 24
(B) 26
(C) 36
(D) 30
Click to View Answer
Correct Answer: [Insert Correct Answer]
2. The number of real roots of the equation  is:
is:
(A) 4
(B) 3
(C) 2
(D) 1
Click to View Answer
Correct Answer: [Insert Correct Answer]
3. Let the set of all values of  , for which both the roots of the equation
, for which both the roots of the equation  are negative real numbers, be the interval
are negative real numbers, be the interval ![(\alpha, \beta]](https://s0.wp.com/latex.php?latex=%28%5Calpha%2C+%5Cbeta%5D&bg=ffffff&fg=000&s=0&c=20201002) . Then
. Then  is equal to:
is equal to:
(A) 5
(B) 6
(C) 0
(D) 9
Click to View Answer
Correct Answer: [Insert Correct Answer]
4. Consider the equation  , where
, where ![n \in [20,100]](https://s0.wp.com/latex.php?latex=n+%5Cin+%5B20%2C100%5D&bg=ffffff&fg=000&s=0&c=20201002) is a natural number. Then the number of all distinct values of
is a natural number. Then the number of all distinct values of  , for which the given equation has integral roots, is equal to:
, for which the given equation has integral roots, is equal to:
(A) 6
(B) 5
(C) 8
(D) 7
Click to View Answer
Correct Answer: [Insert Correct Answer]
5. Let the equation  have equal roots. Then the distance of the point
have equal roots. Then the distance of the point  from the line
from the line  is:
is:
(A) 15
(B) 12
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Answer]
6. Let  and
and 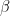 be the roots of
be the roots of  , and
, and 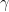 and
and 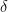 be the roots of
be the roots of  . If
. If  and
and  , then
, then  is equal to:
is equal to:
(A) 4
(B) 3
(C) 5
(D) 7
Click to View Answer
Correct Answer: [Insert Correct Answer]
7. Let  ,
, 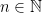 . If
. If  ,
,  ,
,  and
and  , then the quadratic equation having roots
, then the quadratic equation having roots  and
and  is:
is:
(A) 
(B) 
(C) 
(D) 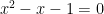
Click to View Answer
Correct Answer: [Insert Correct Answer]
8. If the set of all 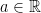 , for which the equation
, for which the equation  has no real root, is the interval
has no real root, is the interval  , and
, and  , then
, then  is equal to:
is equal to:
(A) 2139
(B) 2119
(C) 2109
(D) 2129
Click to View Answer
Correct Answer: [Insert Correct Answer]
9. The number of solutions of the equation  is:
is:
(A) 3
(B) 2
(C) 1
(D) 4
Click to View Answer
Correct Answer: [Insert Correct Answer]
10. Let  be a polynomial of degree 2, satisfying
be a polynomial of degree 2, satisfying  . If
. If  , then the sum of squares of all possible values of
, then the sum of squares of all possible values of 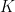 is:
is:
(A) 9
(B) 1
(C) 6
(D) 7
Click to View Answer
Correct Answer: [Insert Correct Answer]
11. The sum of the squares of all the roots of the equation  , is:
, is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Answer]
12. The number of real solution(s) of the equation  is:
is:
(A) 2
(B) 3
(C) 1
(D) 0
Click to View Answer
Correct Answer: [Insert Correct Answer]
13. The product of all the rational roots of the equation  , is equal to:
, is equal to:
(A) 7
(B) 21
(C) 28
(D) 14
Click to View Answer
Correct Answer: [Insert Correct Answer]
14. Let  and
and  be the distinct roots of
be the distinct roots of  ,
,  . If
. If  and
and  are the minimum and the maximum values of
are the minimum and the maximum values of  , then
, then  equals:
equals:
(A) 27
(B) 17
(C) 25
(D) 24
Click to View Answer
Correct Answer: [Insert Correct Answer]
15. If the set of all  , for which the roots of the equation
, for which the roots of the equation  are positive is
are positive is ![(-\infty,-\alpha] \cup [\beta, \gamma)](https://s0.wp.com/latex.php?latex=%28-%5Cinfty%2C-%5Calpha%5D+%5Ccup+%5B%5Cbeta%2C+%5Cgamma%29&bg=ffffff&fg=000&s=0&c=20201002) , then
, then  is equal to:
is equal to:
Click to View Answer
Correct Answer: [Insert Integer Value]
16. If the equation  has equal roots, where
has equal roots, where  and
and  , then
, then  is equal to:
is equal to:
Click to View Answer
Correct Answer: [Insert Integer Value]
17. The number of distinct real roots of the equation  , is:
, is:
Click to View Answer
Correct Answer: [Insert Integer Value]
18. Let  be the solutions of the equation
be the solutions of the equation  and
and  . Then the value of
. Then the value of  is:
is:
Click to View Answer
Correct Answer: [Insert Integer Value]
19. The number of real solutions of the equation  is:
is:
Click to View Answer
Correct Answer: [Insert Integer Value]
20. The number of distinct real roots of the equation  is:
is:
Click to View Answer
Correct Answer: [Insert Integer Value]
SECTION B: Quadratic Equations (Q21-60)
21. Let 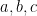 be the lengths of three sides of a triangle satisfying the condition
be the lengths of three sides of a triangle satisfying the condition  . If the set of all possible values of
. If the set of all possible values of  is the interval
is the interval  , then
, then  is equal to:
is equal to:
Click to View Answer
Correct Answer: [Insert Integer Value]
22. The number of real solutions of the equation  is:
is:
Click to View Answer
Correct Answer: [Insert Integer Value]
23. Let  be roots of the equation
be roots of the equation  , where
, where  . If
. If  assumes the minimum possible value, then
assumes the minimum possible value, then  is equal to:
is equal to:
Click to View Answer
Correct Answer: [Insert Integer Value]
24. Let the set  . Then
. Then  is equal to:
is equal to:
Click to View Answer
Correct Answer: [Insert Integer Value]
25. Let ![[\alpha]](https://s0.wp.com/latex.php?latex=%5B%5Calpha%5D&bg=ffffff&fg=000&s=0&c=20201002) denote the greatest integer
denote the greatest integer  . Then
. Then ![[\sqrt{1}]+[\sqrt{2}]+[\sqrt{3}]+\ldots+[\sqrt{120}]](https://s0.wp.com/latex.php?latex=%5B%5Csqrt%7B1%7D%5D%2B%5B%5Csqrt%7B2%7D%5D%2B%5B%5Csqrt%7B3%7D%5D%2B%5Cldots%2B%5B%5Csqrt%7B120%7D%5D&bg=ffffff&fg=000&s=0&c=20201002) is equal to:
is equal to:
Click to View Answer
Correct Answer: [Insert Integer Value]
26. The number of points where the curve  cuts the
cuts the  -axis, is equal to:
-axis, is equal to:
Click to View Answer
Correct Answer: [Insert Integer Value]
27. If  and
and 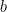 are the roots of the equation
are the roots of the equation  , then the value of
, then the value of  is equal to:
is equal to:
Click to View Answer
Correct Answer: [Insert Integer Value]
28. Let  and
and  be the numbers of real roots of the quadratic equations
be the numbers of real roots of the quadratic equations ![x^{2}-12 x+[x]+31=0](https://s0.wp.com/latex.php?latex=x%5E%7B2%7D-12+x%2B%5Bx%5D%2B31%3D0&bg=ffffff&fg=000&s=0&c=20201002) and
and  respectively, where
respectively, where ![[x]](https://s0.wp.com/latex.php?latex=%5Bx%5D&bg=ffffff&fg=000&s=0&c=20201002) denotes the greatest integer
denotes the greatest integer 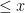 . Then
. Then  is equal to:
is equal to:
Click to View Answer
Correct Answer: [Insert Integer Value]
29. If the value of real number  for which
for which  and
and  have a common real root is
have a common real root is  , then
, then 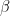 is equal to:
is equal to:
Click to View Answer
Correct Answer: [Insert Integer Value]
30. Let  be the roots of the equation
be the roots of the equation  and
and  . Then
. Then  is equal to:
is equal to:
Click to View Answer
Correct Answer: [Insert Integer Value]
31. Let 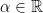 and let
and let 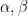 be the roots of the equation
be the roots of the equation  . If
. If  , then the product of all possible values of
, then the product of all possible values of  is:
is:
Click to View Answer
Correct Answer: [Insert Integer Value]
32. Let 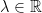 and let the equation
and let the equation 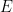 be
be  . Then the largest element in the set
. Then the largest element in the set  is:
is:
Click to View Answer
Correct Answer: [Insert Integer Value]
33. Let  be the roots of the quadratic equation
be the roots of the quadratic equation  . If
. If  , then
, then  is equal to:
is equal to:
Click to View Answer
Correct Answer: [Insert Integer Value]
34. The sum of all real values of  for which
for which  is equal to:
is equal to:
Click to View Answer
Correct Answer: [Insert Integer Value]
35. If for some  , not all have same sign, one of the roots of the equation
, not all have same sign, one of the roots of the equation  is also a root of the equation
is also a root of the equation  , then
, then  is equal to:
is equal to:
Click to View Answer
Correct Answer: [Insert Integer Value]
36. The number of distinct real roots of the equation  is:
is:
Click to View Answer
Correct Answer: [Insert Integer Value]
37. The number of real solutions of the equation  is:
is:
Click to View Answer
Correct Answer: [Insert Integer Value]
38. Let 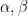 be the roots of the equation
be the roots of the equation  and
and  be the roots of the equation
be the roots of the equation  . If
. If  , then
, then  is equal to:
is equal to:
Click to View Answer
Correct Answer: [Insert Integer Value]
39. If the sum of all the roots of the equation  is
is  , then
, then  is equal to:
is equal to:
Click to View Answer
Correct Answer: [Insert Integer Value]
40. Let  and
and  be two real numbers such that
be two real numbers such that  and
and  . Then
. Then  is equal to:
is equal to:
Click to View Answer
Correct Answer: [Insert Integer Value]
41. The sum of the cubes of all the roots of the equation  is:
is:
Click to View Answer
Correct Answer: [Insert Integer Value]
42. Let  be a polynomial of degree 3 such that
be a polynomial of degree 3 such that  for
for  . Then the value of
. Then the value of  is equal to:
is equal to:
Click to View Answer
Correct Answer: [Insert Integer Value]
43. Let  be in
be in 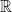 . If
. If  and
and 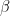 are the roots of the equation
are the roots of the equation  , and
, and  and
and 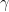 are the roots of equation
are the roots of equation  , then
, then  is equal to:
is equal to:
(A) 36
(B) 9
(C) 27
(D) 18
Click to View Answer
Correct Answer: [Insert Correct Answer]
44. The sum of all integral values of  for which the equation
for which the equation  in
in  has no real roots, is:
has no real roots, is:
Click to View Answer
Correct Answer: [Insert Integer Value]
45. The number of real roots of the equation  is equal to:
is equal to:
Click to View Answer
Correct Answer: [Insert Integer Value]
46. If 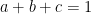 ,
,  and
and  , then the value of
, then the value of  is equal to:
is equal to:
Click to View Answer
Correct Answer: [Insert Integer Value]
47. If 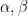 are roots of the equation
are roots of the equation  ,
,  and
and  for each positive integer
for each positive integer  , then the value of
, then the value of  is equal to:
is equal to:
Click to View Answer
Correct Answer: [Insert Integer Value]
48. Let  and
and 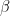 be two real numbers such that
be two real numbers such that  and
and  . Let
. Let  ,
,  and
and  for some integer
for some integer 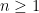 . Then, the value of
. Then, the value of  is:
is:
Click to View Answer
Correct Answer: [Insert Integer Value]
49. The sum of the  power of the roots of the equation
power of the roots of the equation  is:
is:
Click to View Answer
Correct Answer: [Insert Integer Value]
50. The number of real roots of the equation  is:
is:
Click to View Answer
Correct Answer: [Insert Integer Value]
51. The least positive value of  for which the equation
for which the equation  has real roots is:
has real roots is:
Click to View Answer
Correct Answer: [Insert Integer Value]
52. Let  , be the roots of the equation
, be the roots of the equation  . Let
. Let  . Then
. Then  is equal to:
is equal to:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Answer]
53. Let 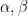 be the roots of the equation
be the roots of the equation  . The quadratic equation, whose roots are
. The quadratic equation, whose roots are  and
and  , is:
, is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Answer]
54. The sum of all the solutions of the equation  is:
is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Answer]
55. Let 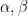 be the distinct roots of the equation
be the distinct roots of the equation  and
and  . Then the minimum value of
. Then the minimum value of  is:
is:
(A) 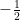
(B) 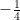
(C) 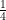
(D) 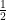
Click to View Answer
Correct Answer: [Insert Correct Answer]
56. The coefficients 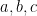 in the quadratic equation
in the quadratic equation  are from the set
are from the set  . If the probability of this equation having one real root bigger than the other is
. If the probability of this equation having one real root bigger than the other is  , then
, then  equals:
equals:
(A) 38
(B) 7
(C) 57
(D) 19
Click to View Answer
Correct Answer: [Insert Correct Answer]
57. If 2 and 6 are the roots of the equation  , then the quadratic equation, whose roots are
, then the quadratic equation, whose roots are  and
and  , is:
, is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Answer]
58. Let  and
and 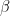 be the roots of the equation
be the roots of the equation  , where
, where  . If
. If 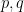 and
and  be the consecutive terms of a non-constant G.P. and
be the consecutive terms of a non-constant G.P. and  , then the value of
, then the value of 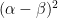 is:
is:
(A) 8
(B) 9
(C) 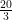
(D) 
Click to View Answer
Correct Answer: [Insert Correct Answer]
59. Let  . Then the number of elements in
. Then the number of elements in  is:
is:
(A) 4
(B) 0
(C) 2
(D) 1
Click to View Answer
Correct Answer: [Insert Correct Answer]
60. Let  be the set of positive integral values of
be the set of positive integral values of  for which
for which  . Then, the number of elements in
. Then, the number of elements in  is:
is:
(A) 0
(B) $\infty$
(C) 3
(D) 1
Click to View Answer
Correct Answer: [Insert Correct Answer]
SECTION C: Quadratic Equations (Q61-80)
61. If 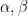 are the roots of the equation
are the roots of the equation  and
and  , then:
, then:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Answer]
62. The number of real roots of the equation  , is:
, is:
(A) 4
(B) 3
(C) 5
(D) 6
Click to View Answer
Correct Answer: [Insert Answer]
63. Let 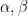 be the roots of the equation
be the roots of the equation  . Then
. Then  is equal to:
is equal to:
(A) -64
(B) 
(C) 
(D) -128
Click to View Answer
Correct Answer: [Insert Answer]
64. The set of all 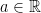 for which the equation
for which the equation  has exactly one real root, is:
has exactly one real root, is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Answer]
65. Let 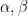 be the roots of the quadratic equation
be the roots of the quadratic equation  . Then
. Then  is equal to:
is equal to:
(A) 72
(B) 9
(C) 729
(D) 81
Click to View Answer
Correct Answer: [Insert Answer]
66. Let  be the three roots of the equation
be the three roots of the equation  . If
. If  , then
, then  is equal to:
is equal to:
(A) 21
(B) 19
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Answer]
67. Let ![A=\{x \in \mathbb{R} : [x+3]+[x+4] \leq 3\}](https://s0.wp.com/latex.php?latex=A%3D%5C%7Bx+%5Cin+%5Cmathbb%7BR%7D+%3A+%5Bx%2B3%5D%2B%5Bx%2B4%5D+%5Cleq+3%5C%7D&bg=ffffff&fg=000&s=0&c=20201002) ,
,  , where
, where ![[t]](https://s0.wp.com/latex.php?latex=%5Bt%5D&bg=ffffff&fg=000&s=0&c=20201002) denotes greatest integer function. Then:
denotes greatest integer function. Then:
(A) 
(B) 
(C) 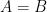
(D) 
Click to View Answer
Correct Answer: [Insert Answer]
68. The sum of all the roots of the equation  is:
is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Answer]
69. The number of integral values of 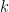 , for which one root of the equation
, for which one root of the equation  lies in the interval $(1,2)$ and its other root lies in the interval $(2,3)$, is:
lies in the interval $(1,2)$ and its other root lies in the interval $(2,3)$, is:
(A) 2
(B) 0
(C) 1
(D) 3
Click to View Answer
Correct Answer: [Insert Answer]
70. Let  . Then
. Then  is equal to:
is equal to:
(A) 6
(B) 4
(C) 0
(D) 2
Click to View Answer
Correct Answer: [Insert Answer]
71. The equation  has:
has:
(A) two solutions and both are negative
(B) two solutions and only one of them is negative
(C) four solutions two of which are negative
(D) no solution
Click to View Answer
Correct Answer: [Insert Answer]
72. The number of real roots of the equation  , is:
, is:
(A) 0
(B) 1
(C) 3
(D) 2
Click to View Answer
Correct Answer: [Insert Answer]
73. Let  be a real number. Let
be a real number. Let 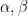 be the roots of the equation
be the roots of the equation  and
and  be the roots of the equation
be the roots of the equation  . Then
. Then  and
and  are the roots of the equation:
are the roots of the equation:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Answer]
74. The number of real solutions of the equation  , is:
, is:
(A) 3
(B) 4
(C) 0
(D) 2
Click to View Answer
Correct Answer: [Insert Answer]
75. The equation ![x^{2}-4 x+[x]+3=x[x]](https://s0.wp.com/latex.php?latex=x%5E%7B2%7D-4+x%2B%5Bx%5D%2B3%3Dx%5Bx%5D&bg=ffffff&fg=000&s=0&c=20201002) , where
, where ![[x]](https://s0.wp.com/latex.php?latex=%5Bx%5D&bg=ffffff&fg=000&s=0&c=20201002) denotes the greatest integer function, has:
denotes the greatest integer function, has:
(A) exactly two solutions in 
(B) no solution
(C) a unique solution in 
(D) a unique solution in 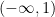
Click to View Answer
Correct Answer: [Insert Answer]
76. If  , then the maximum value of
, then the maximum value of  is:
is:
(A) 198
(B) 202
(C) 212
(D) 218
Click to View Answer
Correct Answer: [Insert Answer]
77. Let ![S=\left\{x \in [-6,3] \setminus \{-2,2\} : \frac{|x+3|-1}{|x|-2} \geq 0\right\}](https://s0.wp.com/latex.php?latex=S%3D%5Cleft%5C%7Bx+%5Cin+%5B-6%2C3%5D+%5Csetminus+%5C%7B-2%2C2%5C%7D+%3A+%5Cfrac%7B%7Cx%2B3%7C-1%7D%7B%7Cx%7C-2%7D+%5Cgeq+0%5Cright%5C%7D&bg=ffffff&fg=000&s=0&c=20201002) and
and  . Then the number of elements in
. Then the number of elements in  is:
is:
(A) 7
(B) 5
(C) 4
(D) 3
Click to View Answer
Correct Answer: [Insert Answer]
78. Let 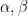 be the roots of the equation
be the roots of the equation  and
and  be the roots of the equation
be the roots of the equation  . Then the roots of the equation
. Then the roots of the equation  are:
are:
(A) non-real complex numbers
(B) real and both negative
(C) real and both positive
(D) real and exactly one of them is positive
Click to View Answer
Correct Answer: [Insert Answer]
79. If 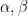 are the roots of the equation
are the roots of the equation  , then the equation, whose roots are
, then the equation, whose roots are  and
and  , is:
, is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Answer]
80. The minimum value of the sum of the squares of the roots of  is:
is:
(A) 4
(B) 5
(C) 6
(D) 8
Click to View Answer
Correct Answer: [Insert Answer]
