Straight Lines
1. Let the area of the triangle formed by a straight line  with co-ordinate axes be 48 square units. If the perpendicular drawn from the origin to the line
with co-ordinate axes be 48 square units. If the perpendicular drawn from the origin to the line 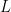 makes an angle of
makes an angle of 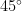 with the positive
with the positive  -axis, then the value of
-axis, then the value of  is:
is:
(A) 90
(B) 83
(C) 93
(D) 97
Click to View Answer
Correct Answer: [Insert Correct Answer]
2. Let the triangle  be the image of the triangle with vertices
be the image of the triangle with vertices  ,
,  and
and  in the line
in the line  . If the centroid of
. If the centroid of  is the point
is the point  , then
, then  is equal to:
is equal to:
(A) 21
(B) 19
(C) 22
(D) 24
Click to View Answer
Correct Answer: [Insert Correct Answer]
3. A rod of length eight units moves such that its ends  and
and  always lie on the lines
always lie on the lines  and
and  , respectively. If the locus of the point
, respectively. If the locus of the point  , that divides the rod
, that divides the rod  internally in the ratio
internally in the ratio  is
is  , then
, then  is equal to:
is equal to:
(A) 24
(B) 22
(C) 21
(D) 23
Click to View Answer
Correct Answer: [Insert Correct Answer]
4. Let the lines  ,
,  , and
, and  be concurrent. If the image of the point
be concurrent. If the image of the point  in the line
in the line  is
is  , then
, then  is equal to:
is equal to:
(A) 91
(B) 113
(C) 101
(D) 84
Click to View Answer
Correct Answer: [Insert Correct Answer]
5. Let the points  lie on or inside the triangle with sides
lie on or inside the triangle with sides  ,
,  and
and  . Then the product of the smallest and the largest values of
. Then the product of the smallest and the largest values of  is equal to:
is equal to:
(A) 22
(B) 33
(C) 55
(D) 44
Click to View Answer
Correct Answer: [Insert Correct Answer]
6. If  and
and  are the points of intersection of the circle
are the points of intersection of the circle  and the hyperbola
and the hyperbola  and a point
and a point  moves on the line
moves on the line  , then the centroid of
, then the centroid of  lies on the line:
lies on the line:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Answer]
7. Two equal sides of an isosceles triangle are along  and
and  . If
. If  is the slope of its third side, then the sum of all possible distinct values of
is the slope of its third side, then the sum of all possible distinct values of  is:
is:
(A) 
(B) 12
(C) -6
(D) 6
Click to View Answer
Correct Answer: [Insert Correct Answer]
8. Let  be a triangle formed by the lines
be a triangle formed by the lines  ,
,  and
and  . Let the point
. Let the point  be the image of the centroid of
be the image of the centroid of  in the line
in the line  . Then
. Then  is equal to:
is equal to:
(A) 47
(B) 37
(C) 40
(D) 36
Click to View Answer
Correct Answer: [Insert Correct Answer]
9. Let the line  meet the axes of
meet the axes of  and
and 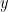 at
at  and
and  , respectively. A right angled triangle
, respectively. A right angled triangle  is inscribed in the triangle
is inscribed in the triangle  , where
, where 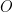 is the origin and the points
is the origin and the points  and
and 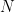 lie on the lines
lie on the lines 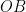 and
and  , respectively. If the area of the triangle
, respectively. If the area of the triangle  is
is 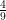 of the area of the triangle
of the area of the triangle  and
and  , then the sum of all possible value(s) of
, then the sum of all possible value(s) of  is:
is:
(A) 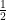
(B) 
(C) 2
(D) 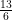
Click to View Answer
Correct Answer: [Insert Correct Answer]
10. A line passes through the origin and makes equal angles with the positive coordinate axes. It intersects the lines  and
and  ,
, 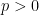 , at the points
, at the points  and
and  , respectively. If
, respectively. If  and the foot of the perpendicular from the point
and the foot of the perpendicular from the point  on the line
on the line 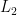 is
is  , then
, then  is equal to:
is equal to:
(A) 5
(B) 3
(C) 2
(D) 4
Click to View Answer
Correct Answer: [Insert Correct Answer]
11. Consider the lines  ,
,  being a parameter, all passing through a point
being a parameter, all passing through a point  . One of these lines (say
. One of these lines (say 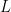 ) is farthest from the origin. If the distance of
) is farthest from the origin. If the distance of 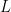 from the point
from the point  is
is  , then the value of
, then the value of  is:
is:
(A) 10
(B) 20
(C) 15
(D) 30
Click to View Answer
Correct Answer: [Insert Correct Answer]
12. Let the three sides of a triangle are on the lines  ,
,  and
and  . Then the distance of its orthocentre from the orthocentre of the triangle formed by the lines
. Then the distance of its orthocentre from the orthocentre of the triangle formed by the lines 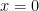 ,
,  and
and  is:
is:
(A) 
(B) 20
(C) 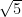
(D) 5
Click to View Answer
Correct Answer: [Insert Correct Answer]
13. Let 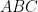 be the triangle such that the equations of lines
be the triangle such that the equations of lines  and
and  be
be  and
and  , respectively, and the points
, respectively, and the points  and
and 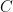 lie on
lie on  -axis. If
-axis. If  is the orthocentre of the triangle
is the orthocentre of the triangle 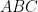 , then the area of the triangle
, then the area of the triangle  is equal to:
is equal to:
(A) 8
(B) 4
(C) 10
(D) 6
Click to View Answer
Correct Answer: [Insert Correct Answer]
14. If the orthocenter of the triangle formed by the lines  ,
,  and
and  is at
is at  , then
, then  is:
is:
(A) 0
(B) 2
(C) -2
(D) 4
Click to View Answer
Correct Answer: [Insert Correct Answer]
15. A line passing through the point  makes an acute angle
makes an acute angle  with the positive
with the positive  -axis. Let this line be rotated about the point
-axis. Let this line be rotated about the point  through an angle
through an angle  in the clockwise direction. If in the new position, the slope of the line is
in the clockwise direction. If in the new position, the slope of the line is 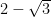 and its distance from the origin is
and its distance from the origin is  , then the value of
, then the value of  is:
is:
(A) 8
(B) 4
(C) 5
(D) 6
Click to View Answer
Correct Answer: [Insert Correct Answer]
16. Let  be the length of a side of a square
be the length of a side of a square  with
with 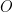 being the origin. Its side
being the origin. Its side 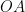 makes an acute angle
makes an acute angle  with the positive
with the positive  -axis and the equations of its diagonals are
-axis and the equations of its diagonals are  and
and  . Then
. Then 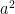 is equal to:
is equal to:
(A) 48
(B) 16
(C) 24
(D) 32
Click to View Answer
Correct Answer: [Insert Correct Answer]
17. A variable line 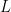 passes through the point
passes through the point  and intersects the positive coordinate axes at the points
and intersects the positive coordinate axes at the points  and
and  . The minimum area of the triangle
. The minimum area of the triangle  , where
, where 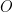 is the origin, is:
is the origin, is:
(A) 35
(B) 25
(C) 30
(D) 40
Click to View Answer
Correct Answer: [Insert Correct Answer]
18. A ray of light coming from the point  gets reflected from the point
gets reflected from the point 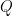 on the
on the  -axis and then passes through the point
-axis and then passes through the point  . If the point
. If the point  is such that
is such that  is a parallelogram, then
is a parallelogram, then  is equal to:
is equal to:
(A) 60
(B) 70
(C) 80
(D) 90
Click to View Answer
Correct Answer: [Insert Correct Answer]
19. If the line segment joining the points  and
and  subtends an angle
subtends an angle 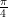 at the origin, then the absolute value of the product of all possible values of
at the origin, then the absolute value of the product of all possible values of  is:
is:
(A) 4
(B) 8
(C) 6
(D) 2
Click to View Answer
Correct Answer: [Insert Correct Answer]
20. The equations of two sides  and
and  of a triangle
of a triangle 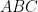 are
are  and
and  , respectively. The point
, respectively. The point  divides the third side
divides the third side  internally in the ratio
internally in the ratio  , the equation of the side
, the equation of the side  is:
is:
(A) 
(B) 
(C) 
(D) 
Click to View Answer
Correct Answer: [Insert Correct Answer]
